trabajo realizado en el ciclo 2023-II. Profesor: Jeronimo Garcia
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results

Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Calculo de la qi (segun Formula Garcia)
Run to view results
Run to view results

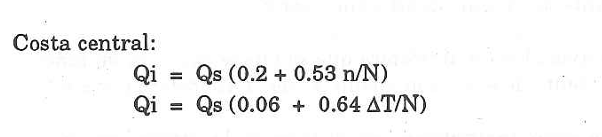
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
interpolación de PM
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results

Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
se puede mejorar la Tmedia del aire
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results
Run to view results