Discrete random systems

Realizado por: Jorge Ramos, Emil Encalda, Stheeven Quishpe

Asigantura: Modelos y Simulación

¿Qué es la percolación?

La percolación es una idea utilizada en probabilidad y física estadística que describe cómo un fluido, una señal o cualquier fenómeno similar logra moverse a través de un material o sistema compuesto por zonas que permiten el paso y zonas que lo bloquean.

Para estudiarla, normalmente se representa el sistema como una rejilla o malla, donde cada punto puede estar:

El interés principal es descubrir si existe un camino continuo formado solo por puntos abiertos que conecte un extremo del sistema con otro (por ejemplo, de arriba hacia abajo).

¿Cómo se genera el grid y cómo comprobamos si percola?

Para esta simulación utilizamos una malla cuadrada de 2×2, donde cada celda se modela como un valor binario que indica si permite o no el paso:

1 → celda abierta

0 → celda cerrada

Generación del grid

El grid se construye de manera aleatoria. Para cada celda se genera un número uniforme en el intervalo[0,1] y se compara con una probabilidad p:

grid = np.random.rand(2, 2) < p

Esto significa que:

En otras palabras, el patrón de celdas abiertas/cerradas cambia en cada ejecución siguiendo esa probabilidad.

Verificación de la percolación

En un sistema tan pequeño como una malla de 2×2, la comprobación es sencilla: se debe determinar si existe algún camino vertical completamente formado por celdas abiertas que conecte la fila superior con la inferior.

Para este caso reducido, las posibles rutas se pueden revisar directamente, ya que solo existen unas pocas combinaciones. Si al menos una de ellas está compuesta únicamente por celdas abiertas, entonces decimos que el grid percola.

¿Qué es la probabilidad teórica de percolación?

En un sistema tan pequeño como una malla de 2×2, es posible calcular la probabilidad de percolación de forma exacta. La probabilidad teórica corresponde a la proporción de configuraciones del grid que permiten un camino vertical completamente abierto entre la parte superior y la inferior.

Dado que cada celda está abierta con probabilidad p, y cerrada con probabilidad 1−p, se pueden enumerar todas las combinaciones posibles y determinar en cuáles aparece un camino válido. A partir de ese análisis se obtiene una expresión cerrada para la probabilidad de que el sistema percole.

Ejercicio 1 :

Calcular la probabilidad de que a 2 x 2 sistemas percolada is p^2 * (2 - p^2) where p is la probabilidad que un lugar esta abierto

Calcule la probabilidad de percolación para 𝑝∈{0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9}.

A través de este bloque de código se define la función que evalúa si una matriz 2×2 percola. Luego se crea la lista p_values, que contiene varios valores de probabilidad entre 0 y 1. Finalmente, un ciclo for recorre cada valor de p en p_values y utiliza la función de percolación para calcular la probabilidad correspondiente para cada p.

Se define una función que simula la percolación. Dentro de ella se inicia un contador de percolaciones exitosas y, mediante un bucle for, se repite el experimento tantas veces como se indique. En cada repetición se genera un grid aleatorio según la probabilidad 𝑝 y se revisan sus columnas. Si alguna está completamente abierta, se suma una percolación y se detiene la revisión con break. Al final, la función devuelve la fracción de repeticiones en las que el sistema percoló.

El código también incluye una sección para graficar los resultados. Luego, otro ciclo for recorre los valores de p_values, ejecuta la simulación para cada 𝑝 y produce la gráfica correspondiente.

Después de obtener las probabilidades simuladas y la curva teórica, se realiza una comparación entre ambas. Para ello se ejecutan simulaciones con distintos números de grids: 1, 10, 100 y 1000. Estos valores se añaden al gráfico, permitiendo ver cómo la estimación empírica se acerca cada vez más a la probabilidad teórica conforme aumenta la cantidad de simulaciones.

¿Qué se simula y cómo se mide el resultado?

Entrada del sistema:

Salida del sistema:

La proporción de grids que percolan, es decir:

percolaciones exitosas/total de simulaciones

Método de medición:

¿Qué es la distancia de Hamming?

Es el número de posiciones distintas entre dos cadenas o vectores del mismo tamaño.

Ejemplo: 1010 vs 0011 → difieren en 2 posiciones → distancia = 2.

¿Por qué la medimos?

Porque sirve para:

Detectar y corregir errores en códigos binarios.

Comparar similitud entre secuencias (genéticas, datos, etc.).

Identificar diferencias en patrones usados en IA y computación.

Ejercicio 2:

Generate Random binary vectors where P( X = 1) = a

Calcular la distancia de hamming entre cualquier 2 vectores aleatorios

Try a∈{0.0, 0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0}.

En esta parte se crean dos funciones: una genera vectores binarios aleatorios y la otra calcula la distancia de Hamming entre dos vectores. El cálculo se realiza comparando cada posición y sumando cuántos elementos difieren, usando operaciones vectorizadas de NumPy.

Se crea una función que calcula la distancia de Hamming media entre varios vectores binarios. Primero genera los vectores y luego usa dos bucles anidados para comparar cada par posible. En cada comparación suma la distancia de Hamming. Al final, divide la suma total entre el número de comparaciones y devuelve la distancia promedio.

¿Cómo se genera el sistema de vectores?

Los vectores se generan de forma aleatoria usando una distribución Bernoulli: cada bit es 1 con probabilidad a y 0 con probabilidad 1 − a. La longitud del vector es fija y se repite este proceso para crear todos los vectores del sistema. El valor de a se va variando entre 0 y 1 para analizar cómo afecta a la distancia media de Hamming.

¿Cómo se mide la distancia media de Hamming?

La distancia media de Hamming se mide así:

Entrada:

Probabilidad a de que un bit sea 1.

Número de vectores a generar.

Tamaño de cada vector.

Proceso:

Se generan varios vectores binarios usando la probabilidad a.

Se calcula la distancia de Hamming entre cada par de vectores.

Se promedian todas las distancias obtenidas.

Resultado teórico: La distancia media esperada entre dos vectores de tamaño n es:

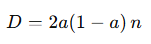
que corresponde a la probabilidad de que dos bits difieran multiplicada por la longitud del vector.

¿Qué y cómo se representa gráficamente?

Ejercicio 3:

Ahora explicaremos como conseguimos las compraciones con 1,10,100,1000 comparaciones

En este segmento del código se utiliza un bucle for que itera sobre los diferentes valores de 𝑎, guardando en la variable simulated_results los valores obtenidos de la distancia media de Hamming para cada caso. Posteriormente, se genera una gráfica que muestra los resultados simulados en función de 𝑎. El resto del código se encarga del formato y la visualización del gráfico.

Este bloque de código usa un bucle for que repite el cálculo de la distancia media de Hamming varias veces y guarda cada resultado en simulated_results. Luego, con esos valores, se genera una gráfica que muestra cómo varía la distancia media según las simulaciones. El resto del código solo se encarga de dibujar y mostrar el gráfico.

Conclusiones

La simulación confirma el modelo teórico en el sistema 2×2. Los valores obtenidos por medio de las simulaciones coinciden con la fórmula de percolación, especialmente cuando aumenta el número de pruebas. Esto muestra que incluso en modelos pequeños, el comportamiento teórico se refleja en la práctica.

La distancia media de Hamming es máxima cuando P(X=1)=0.5. Los resultados evidencian que la mayor diferencia entre vectores binarios ocurre cuando la probabilidad de obtener un 1 es del 50 %. Esto coincide con la expresión teórica E[d]=2a(1−a)n, que describe una relación simétrica entre probabilidad y variabilidad.

Más repeticiones producen resultados más precisos. Al aumentar la cantidad de simulaciones (1, 10, 100, 1000), los valores obtenidos se vuelven más estables y se acercan al resultado teórico esperado. Esto confirma que un mayor tamaño de muestra mejora la confiabilidad en experimentos probabilísticos.