Generate continuous random variables
Realizado por: Jorge Ramos, Daniel Encalada, Stheeven Quishpe
Asignatura: Modelos y Simulación
Introducción
La generación de variables aleatorias es una herramienta clave en la simulación computacional, ya que permite representar fenómenos y sistemas con comportamiento incierto. En este proyecto se desarrollan y comparan dos técnicas ampliamente utilizadas para producir variables aleatorias continuas: el método de Transformación Inversa y el método de Rechazo. Ambos se aplican a dos distribuciones particulares con el fin de evaluar su funcionamiento y utilidad práctica.
Generación de Variables Aleatorias (RVG)
La generación de variables aleatorias permite obtener muestras que siguen distribuciones de probabilidad específicas. Esta capacidad es fundamental en numerosos campos, especialmente en:
Métodos Implementados
1. Muestreo por Transformación Inversa (ITS)
Este método se basa en utilizar la función de distribución acumulada (CDF) y su inversa.
2. Método de Rechazo (RM)
Consiste en generar valores a partir de una distribución auxiliar y aceptar o rechazar muestras según un criterio probabilístico.
Implementación
En este proyecto, ambos métodos se aplican para generar muestras de una Distribución Exponencial Doble, permitiendo comparar su desempeño y precisión en un caso práctico.
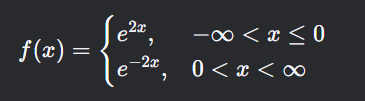
Run to view results
Gráficos Comparativos de Distribuciones
La evaluación visual de los generadores se realiza mediante dos gráficos por cada distribución estudiada (Exponencial Doble y Triangular):
Análisis de la Distribución Exponencial Doble
PDF (gráfico izquierdo)
Línea roja: representa la densidad teórica: f(x) = e^(2x) para x ≤ 0 y f(x) = e^(-2x) para x > 0
Barras del histograma: corresponden a las 10 000 muestras generadas mediante ITS.
Observaciones:
El histograma replica con buena precisión la forma simétrica de la distribución.
El valor máximo ocurre en x=0.
La caída exponencial hacia ambos lados se observa de manera clara.
CDF (gráfico derecho)
Línea roja: muestra la CDF teórica.
Curva escalonada azul: acumulado empírico de las muestras.
Interpretación:
La curva empírica sigue de forma cercana a la teórica.
El punto donde F(x) = 0.5 identifica correctamente la mediana.
La similitud entre ambas curvas confirma el buen desempeño del generador.
Tabla de Resultados Numéricos
La tabla resume la distancia absoluta entre el histograma y la PDF para distintos tamaños de muestra.
Patrones observados:
Gráfico de Convergencia en Escala Log-Log
El gráfico de convergencia permite visualizar cómo decrece el error para cada método y distribución.
Características:
Ambos ejes están en escala logarítmica.
Cada línea representa una combinación método–distribución.
Los puntos marcan los resultados para cada tamaño de muestra.
Interpretación:
Todas las curvas descienden, lo que evidencia que el error disminuye con más muestras.
Una pendiente aproximada a –0.5 coincide con el comportamiento típico 𝑂(1/𝑛).
ITS mantiene valores de error menores que RM, en especial para tamaños pequeños.
Las diferencias entre ambos métodos se reducen a partir de 𝑛 > 10.000 .
Comparación por Distribución
Exponencial Doble
ITS vs RM:
ITS se ajusta mejor en la zona central alrededor de x=0.
RM tiende a producir una ligera subrepresentación en las colas (x <− 3 y 𝑥 > 3x > 3).
Retos particulares:
La discontinuidad en la derivada en x=0 puede afectar la precisión.
Las colas exponenciales requieren más muestras para representar su forma con fidelidad.
Distribución Triangular
Comportamiento general:
Ambos métodos capturan los cambios de pendiente en x=3.
La moda en x = 3 aparece claramente marcada.
Ventaja del ITS:
Reproduce exactamente los puntos clave (x=2, x=3, x=6).
Evita pérdidas de eficiencia relacionadas con el rechazo de muestras.
Conclusiones Generales
Elección del método:
Importancia del tamaño de muestra: