Generational Relevance of Recent Overdose Reductions

This notebook walks through analysis of changes in overdose deaths between 2022 and 2024. Deaths are analyzed by year of birth to see if generational effects are evident in the reduction in overdose. This notebook allows you to reproduce the entire analysis and generate the figure. You can skip the code boxes if you wish, or if you use a different coding language follow the # green comments to see what was done step-by-step.

Notebook created by Nabarun Dasgupta @ UNC Opioid Data Lab (nab@unc.edu) on May 28-9, 2025

Written in Python 3.10 for Data Science

We have 3 data limitations to contend with.

CDC NVSS data don't have demographics, are predicted, and smoothed. So trends, by definition, will get obliterated. Therefore, we must use CDC WONDER data.

CDC WONDER Cell counts between 1-9 are suppressed, meaning if there are 3 deaths in 2023 among 6 year-olds, then we wouldn't be able to observe them.

Deaths investigations for the last months of 2024 are still pending, leading to incomplete "provisional" data. But we can look at data from previous years to see how likely this delay is, and adjust for it mathematically.

Data Import

Load month x age-at-death from WONDER. Specifications below:

Dataset: Provisional Mortality Statistics, 2018 through Last Week Query Parameters: UCD - Drug/Alcohol Induced Causes: Drug poisonings (overdose) Unintentional (X40-X44); Drug poisonings (overdose) Suicide (X60-X64); Drug poisonings (overdose) Homicide (X85); Drug poisonings (overdose) Undetermined (Y10-Y14) Year/Month: 2022; 2023; 2024 (provisional) Group By: Single-Year Ages; Month Show Totals: Disabled Show Zero Values: True Show Suppressed: True Calculate Rates Per: 100,000 Rate Options: Default intercensal populations for years 2001-2009 (except Infant Age Groups) --- Help: See http://wonder.cdc.gov/wonder/help/mcd-provisional.html for more information. --- Query Date: May 28, 2025 7:57:26 PM --- Suggested Citation: Centers for Disease Control and Prevention, National Center for Health Statistics. National Vital Statistics System, Provisional Mortality on CDC WONDER Online Database. Data are from the final Multiple Cause of Death Files, 2018-2023, and from provisional data for years 2024 and later, as compiled from data provided by the 57 vital statistics jurisdictions through the Vital Statistics Cooperative Program. Accessed at http://wonder.cdc.gov/mcd-icd10-provisional.html on May 28, 2025 7:57:26 PM

The original CSV for analysis can be downloaded from the block below, using the arrow in the bottom right corner.

import pandas as pd # Load the monthly OD data CSV file into a pandas DataFrame file_path = "od-annual-age-year.csv" df = pd.read_csv(file_path) # Convert "2024 (provisional)" to "2024" and make the Year column numeric df['Year'] = df['Year'].replace("2024 (provisional)", "2024") df['Year'] = pd.to_numeric(df['Year']) df

File and dataframe names:

Handle suppressed values via backfill

df age- and month-level original import from CDC WONDER

df_annual age and year-level original import from CDC WONDER

Load annual counts to backfill suppressed values in monthly counts, with assumption of uniform distribution. Suppression happens if call count is between 1 and 9 cases. So we will assume n=5 for backfilling because it is the midpoint of the suppressed range (1-9).

df_yearsum summed annual values from monthly data to compare to annual; determines impact of suppression rules at single-year level

df_adj is original 'df' adjusted for suppression rules by backfilling from annual data, with assumptions (see below)

We wouldn't have to do this if we could just get actual line-level data from CDC. We need easier, faster data access to answer our questions! Anybody know any government efficiency experts, ha.

df_age building off 'df_adj'; doubly adjusted for backfilled suppression as well as reporting lag from incomplete autopsies (see below). This is the fully adjusted dataset for most analyses.

# Create df_annual from df df_annual = df.copy() # Count rows to be replaced rows_to_replace = df_annual['Deaths'].isin(["Suppressed"]).sum() + df_annual['Deaths'].isna().sum() # Convert Deaths to numeric, coercing errors to NaN df_annual['Deaths'] = pd.to_numeric(df_annual['Deaths'], errors='coerce') # If Deaths is NaN, then backfill with 5 def backfill_with_five(value): if pd.isna(value): return 5 return value df_annual['Deaths'] = df_annual['Deaths'].apply(backfill_with_five) # Filter to display backfilled rows only backfilled_rows = df_annual[df['Deaths'].isna()] print(f"Number of rows replaced with backfill: {rows_to_replace}") backfilled_rows

These are the final confirmed death counts for 2022 and 2023, as close to "truth" as we can get within the national mortality data system.

Handle incomplete or provisional for 2024

As Kastalia Medrano at Filter points out, the NVSS predicted total is usually an overcount by a few thousand. We can see this in 2023 data, which confirmed count is 105,070 whereas it had been predicted to be 110,037, or 4.72%. For 2024, the corresponding predicted is 80,391, but the confirmed cases are 71,903 as of this data analysis on May 28, 2025. Part of this discrepancy is due to pending death investigations.

CDC NCSS notes: "Relative to final data, 12-month ending provisional counts of drug overdose deaths for 2023 were 95% to 96.9% complete after a 4-month lag."

We are now just beyond that 4-month lag.

But this is confusing. One process leads to a 4.72% overestimate, and ones process leads to a 3.1-5.0% underestimate. Which do we adjust for will depend on which data source we want to visualize, the predicted-smoothed or the actuals, respectively. I think actuals.

It's important to note that on the absolute scale there the same order of magnitude fewer deaths, which is what we are really trying to get at in this analysis:

Predicted and smoothed: 80,391 - 110,037 = -29,646

Suppression-removed actuals as they currently stand: 71,903 - 105,102 = -33,199

But this exaggerates the decline because some investigations are still pending. So we can inflate 71,903 suppression-removed confirmed cases up to account for this. CA, TX, NY had the biggest declines in 2024 on the absolute scale (see our post about this), so let's average the 4-month reported (in)complete table from 2023 for these 3 states: 95.9%, 97.3%, 94.3%, respectively. So that 4.2% incomplete on average. This method is better on the absolute scale than taking the average of all states, because smaller states who get their autopsies done quicker would shrink the adjustment.

Putting it all together, 71,903 * 4.2% = 74,922 deaths we predict in 2024.

Suppression-removed & incomplete-adjusted actuals: 74,922 - 105,102 = -30,108 fewer deaths in 2024 vs. 2023

We are going to move ahead with this adjusted figure to get to the heart of the analysis. We will call this our "adjusted" analysis. This is our target total count for 2024 (also known as a marginal sum), and we want to adjust the ageyear-level data accordingly to account for the higher incomplete cases in the last 4 months of the year. We don't have any reason to assume linearity, and in fact our experience tells us this is not linear, so we will fit a quadratic decay to distribute the balance across ages and months to reach the marginal sum.

Makes assumption of uniform birth distribution throughout the calendar year. YOB may be off by plus or minus 6 months for half the population for any given individual, but should be about correct on average.

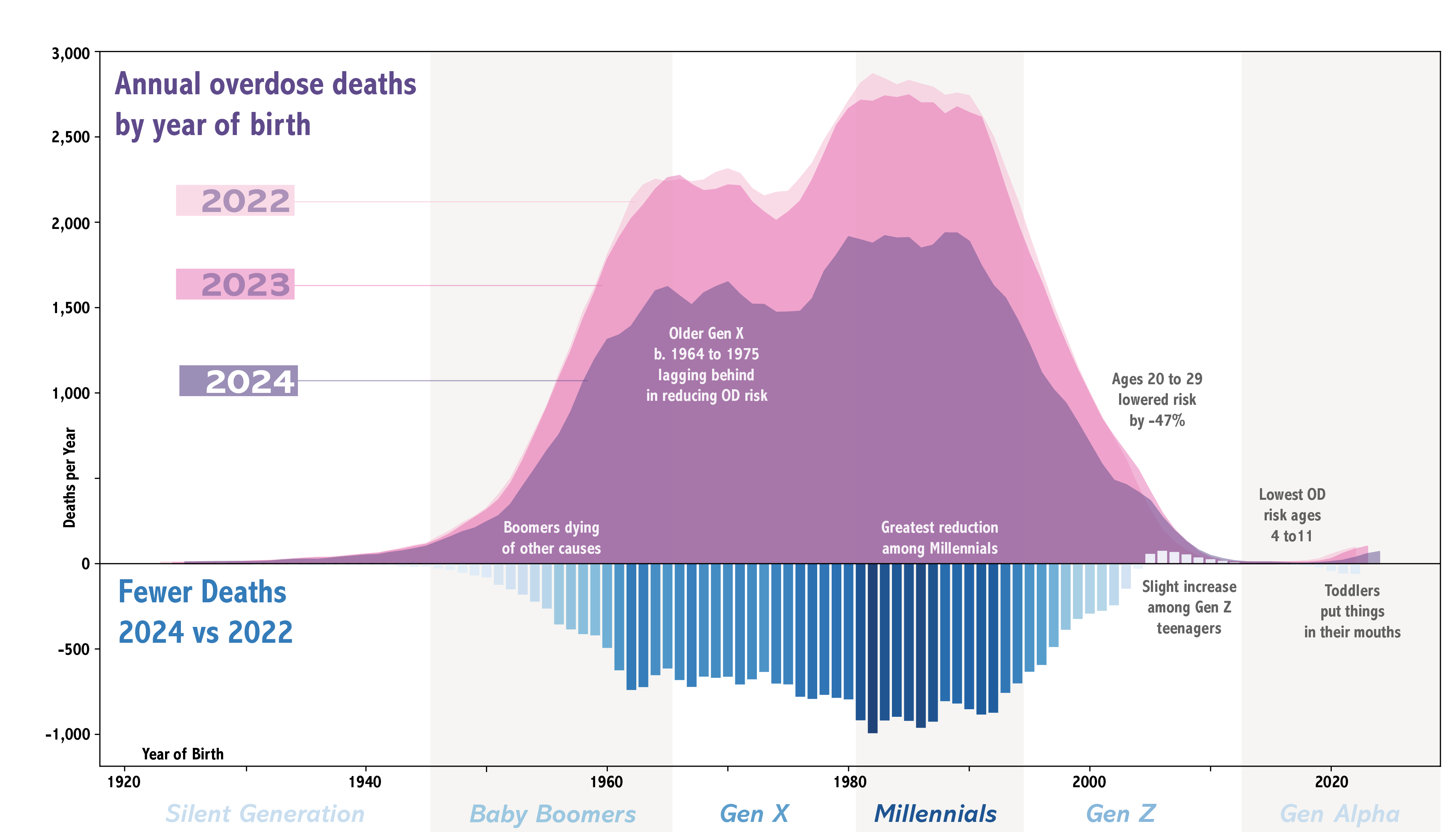
# Generate a new column 'yob' (year of birth) inferred from death month, year, and single-year ages # Extract numeric age from 'Single-Year Ages' column def extract_numeric_age(age_str): try: return int(age_str.split()[0]) # Extract the numeric part of the age except: return 0 # Default to 0 for '< 1 year' or invalid entries df_age['Numeric Age'] = df_age['Single-Year Ages'].apply(extract_numeric_age) # Calculate yob using the numeric age df_age['yob'] = df_age['Year'] - df_age['Numeric Age'] df_age

Year of Birth

import matplotlib.pyplot as plt # Calculate the sum of Deaths by yob deaths_by_yob = df_age.groupby('yob')['Deaths'].sum() # Sort the data by yob deaths_by_yob = deaths_by_yob.sort_index() # Create a vertical bar chart plt.figure(figsize=(8, 6)) plt.bar(deaths_by_yob.index, deaths_by_yob.values, color='skyblue') plt.ylabel('Total Deaths (Adjusted)') plt.xlabel('Year of Birth (yob)') plt.title('Total Adjusted Deaths by Year of Birth') plt.grid(axis='y', linestyle='--', alpha=0.7) plt.tight_layout() plt.show()

# Generalize the code to handle any years in the dataset import matplotlib.pyplot as plt # Get the unique years in the dataset years = df_age['Year'].unique() # Create a dictionary to store the sum of Deaths_adj by yob for each year yob_data = {} for year in years: yob_data[year] = df_age[df_age['Year'] == year].groupby('yob')['Deaths'].sum().sort_index() # Determine the global min and max for both axes all_yobs = pd.concat(yob_data.values()) y_min, y_max = 0, all_yobs.max() x_min, x_max = min(min(data.index) for data in yob_data.values()), max(max(data.index) for data in yob_data.values()) # Create a multi-panel bar chart with one panel for each year fig, axes = plt.subplots(len(years), 1, figsize=(12, 5 * len(years)), sharex=True) # Ensure axes is iterable even if there's only one year if len(years) == 1: axes = [axes] # Plot each year's data in a separate panel for ax, year in zip(axes, years): ax.bar(yob_data[year].index, yob_data[year].values, color='skyblue') ax.set_ylabel('Total Deaths (Adjusted)') ax.set_title(f'Total Adjusted Deaths by Year of Birth ({year})') ax.grid(axis='y', linestyle='--', alpha=0.7) ax.set_xlim(x_min, x_max) ax.set_ylim(y_min, y_max) # Set the x-axis label on the last panel axes[-1].set_xlabel('Year of Birth (yob)') plt.tight_layout() plt.show()

# Extract data for 2022, 2023, and 2024 by age age_2022 = df_age[df_age['Year'] == 2022].groupby('Numeric Age')['Deaths'].sum() age_2023 = df_age[df_age['Year'] == 2023].groupby('Numeric Age')['Deaths'].sum() age_2024 = df_age[df_age['Year'] == 2024].groupby('Numeric Age')['Deaths'].sum() # Calculate the difference in deaths by age between 2022 and 2024 difference_by_age = age_2024 - age_2022 # Create a vertical bar chart with three series: 2022, 2023, and 2024 plt.figure(figsize=(14, 8)) # Plot 2022 deaths plt.bar(age_2022.index - 0.2, age_2022.values, width=0.4, label='2022', color='teal') # Plot 2023 deaths plt.bar(age_2023.index, age_2023.values, width=0.4, label='2023', color='skyblue') # Plot 2024 deaths plt.bar(age_2024.index + 0.2, age_2024.values, width=0.4, label='2024', color='orange') # Plot the difference as a line plt.plot(difference_by_age.index, difference_by_age.values, label='Difference (2024 - 2022)', color='red', marker='o') # Add labels, title, and legend plt.xlabel('Age') plt.ylabel('Total Deaths (Adjusted)') plt.title('Comparison of Adjusted Deaths by Age: 2022 to 2024') plt.axhline(0, color='black', linewidth=0.8, linestyle='--') plt.legend() plt.grid(axis='y', linestyle='--', alpha=0.7) plt.gca().invert_xaxis() # Invert the x-axis to go from older on the left to younger on the right plt.tight_layout() plt.show()

# Fixing the issue by defining yob_2024, yob_2023, and yob_2022 from the yob_data dictionary # Ensure yob_data dictionary contains data for all years # Extract data for 2022, 2023, and 2024 yob_2022 = yob_data.get(2022, pd.Series(dtype=int)) yob_2023 = yob_data.get(2023, pd.Series(dtype=int)) yob_2024 = yob_data.get(2024, pd.Series(dtype=int)) # Calculate the difference in deaths by yob between 2022 and 2024 difference_by_yob = yob_2024 - yob_2022 # Create a bar chart with three series: 2022, 2023, and 2024 plt.figure(figsize=(14, 8)) # Plot 2022 deaths plt.bar(yob_2022.index - 0.2, yob_2022.values, width=0.4, label='2022', color='teal') # Plot 2023 deaths plt.bar(yob_2023.index, yob_2023.values, width=0.4, label='2023', color='skyblue') # Plot 2024 deaths plt.bar(yob_2024.index + 0.2, yob_2024.values, width=0.4, label='2024', color='orange') # Plot the difference as a line plt.plot(difference_by_yob.index, difference_by_yob.values, label='Difference (2024 - 2022)', color='red', marker='o') # Add labels, title, and legend plt.xlabel('Year of Birth (yob)') plt.ylabel('Total Deaths (Adjusted)') plt.title('Comparison of Adjusted Deaths by Year of Birth: 2022 to 2024') plt.axhline(0, color='black', linewidth=0.8, linestyle='--') plt.legend() plt.grid(axis='y', linestyle='--', alpha=0.7) plt.tight_layout() plt.show()

# Print the title or header before displaying the table print("Limiting to OD decedents born 2000 to 2020") print("Comparing number of deaths by year of birth 2024 vs. 2022") print("Absolute differences between 2024 vs. 2022 (positive (red) means higher in 2024) in table below") # Filter the difference_by_yob_df DataFrame to include only rows where 'Year of Birth (yob)' is between 2000 and 2020 filtered_difference_by_yob_df = difference_by_yob_df.loc[(difference_by_yob_df['Year of Birth (yob)'] >= 2000) & (difference_by_yob_df['Year of Birth (yob)'] <= 2020)].copy() # Round the differences to integers filtered_difference_by_yob_df['Difference in Deaths (2024 - 2022)'] = filtered_difference_by_yob_df['Difference in Deaths (2024 - 2022)'].round().astype(int) # Add 2022 and 2024 counts to the filtered DataFrame and convert them to integers filtered_difference_by_yob_df['Deaths in 2022'] = filtered_difference_by_yob_df['Year of Birth (yob)'].map(yob_2022).round().astype(int) filtered_difference_by_yob_df['Deaths in 2024'] = filtered_difference_by_yob_df['Year of Birth (yob)'].map(yob_2024).round().astype(int) # Display the updated DataFrame filtered_difference_by_yob_df

# Apply a 3-year moving average smoother to the yob data # Ensure yob_data dictionary contains data for all years # Extract data for 2022, 2023, and 2024 yob_2022 = yob_data.get(2022, pd.Series(dtype=int)) yob_2023 = yob_data.get(2023, pd.Series(dtype=int)) yob_2024 = yob_data.get(2024, pd.Series(dtype=int)) # Apply a 3-year moving average smoother def smooth_series(series): return series.rolling(window=3, center=True, min_periods=1).mean() yob_2022_smoothed = smooth_series(yob_2022) yob_2023_smoothed = smooth_series(yob_2023) yob_2024_smoothed = smooth_series(yob_2024) # Calculate the difference in deaths by yob between 2022 and 2024 (smoothed) difference_by_yob_smoothed = yob_2024_smoothed - yob_2022_smoothed # Normalize the differences for coloring and invert the color ramp norm = plt.Normalize(difference_by_yob_smoothed.min(), difference_by_yob_smoothed.max()) colors = plt.cm.Blues_r(norm(difference_by_yob_smoothed.values)) # Use Blues_r for inverted color ramp # Create a plot with transparent solid layers for each year plt.figure(figsize=(14, 8)) # Plot 2022 smoothed deaths plt.fill_between(yob_2022_smoothed.index, yob_2022_smoothed.values, label='2022 (Smoothed)', color='#F5C1D7', alpha=0.6) # Pantone 13-2804 # Plot 2023 smoothed deaths plt.fill_between(yob_2023_smoothed.index, yob_2023_smoothed.values, label='2023 (Smoothed)', color='#E56DB1', alpha=0.5) # Pantone 17-2230 # Plot 2024 smoothed deaths plt.fill_between(yob_2024_smoothed.index, yob_2024_smoothed.values, label='2024 (Smoothed)', color='#5F4B8B', alpha=0.5) # Pantone 19-2630 # Plot the smoothed difference as vertical bars with inverted gradient colors plt.bar(difference_by_yob_smoothed.index, difference_by_yob_smoothed.values, label='Difference (2024 - 2022, Smoothed)', color=colors, alpha=0.9) # Add labels, title, and legend plt.xlabel('Year of Birth', fontsize=14) plt.ylabel('Annual Deaths', fontsize=14) plt.title('Year of Birth Among OD Decedents', fontsize=16) plt.axhline(0, color='black', linewidth=0.9, linestyle='-') #plt.grid(axis='y', linestyle='--', alpha=0.7, zorder=0) # grid lines are behind the plots # Increase font size of axis tick labels plt.xticks(fontsize=16) plt.yticks(fontsize=16) plt.tight_layout() plt.show()

Absolute differences between 2024 vs. 2022 (negative means higher in 2022), before smoothing:

Generations

# Define generational boundaries # Source: Pew Research Center definitions # Note: Adjust boundaries as necessary based on the dataset's context generations = { 'Greatest Generation': (1901, 1927), 'Silent Generation': (1928, 1945), 'Baby Boomers': (1946, 1964), 'Generation X': (1965, 1980), 'Millennials': (1981, 1996), 'Generation Z': (1997, 2012), 'Generation Alpha': (2013, 2025) } # Create a new column 'Generation' in df_age def assign_generation(yob): for generation, (start, end) in generations.items(): if start <= yob <= end: return generation return 'Unknown' df_age['Generation'] = df_age['yob'].apply(assign_generation) # Filter for the year 2024 and group by Generation generation_deaths_2024 = df_age[df_age['Year'] == 2024].groupby('Generation')['Deaths'].sum().reset_index() # Rename columns for clarity generation_deaths_2024.columns = ['Generation', 'Total Deaths in 2024'] # Add a column for the years of each generation def get_generation_years(generation): if generation in generations: start, end = generations[generation] return f"{start}-{end}" return 'Unknown' generation_deaths_2024['Years'] = generation_deaths_2024['Generation'].apply(get_generation_years) # Convert deaths to integers generation_deaths_2024['Total Deaths in 2024'] = generation_deaths_2024['Total Deaths in 2024'].astype(int) # Calculate the percentage of total deaths for each generation total_deaths_2024 = generation_deaths_2024['Total Deaths in 2024'].sum() generation_deaths_2024['Percentage of Total'] = (generation_deaths_2024['Total Deaths in 2024'] / total_deaths_2024 * 100).round(1).astype(str) + '%' # Sort by the order of generations in terms of time generation_deaths_2024['Generation Order'] = generation_deaths_2024['Generation'].map(lambda x: list(generations.keys()).index(x)) generation_deaths_2024 = generation_deaths_2024.sort_values(by='Generation Order').drop(columns=['Generation Order']) # Suppress display of row numbers generation_deaths_2024.style.hide(axis='index')

save plt as editable PDF

# Print the title or header before displaying the table print("Absolute differences between 2024 vs. 2022 (negative means higher in 2022):") # Convert the difference_by_yob Series to a DataFrame for better tabular representation difference_by_yob_df = difference_by_yob.reset_index() difference_by_yob_df.columns = ['Year of Birth (yob)', 'Difference in Deaths (2024 - 2022)'] # Display the DataFrame difference_by_yob_df

# Save the last plot as an editable PDF without the IRR panel and without the legend fig, ax1 = plt.subplots(figsize=(14, 8)) # Plot 2022 smoothed deaths on the axis ax1.fill_between(yob_2022_smoothed.index, yob_2022_smoothed.values, color='#F5C1D7', alpha=0.6) # Plot 2023 smoothed deaths on the axis ax1.fill_between(yob_2023_smoothed.index, yob_2023_smoothed.values, color='#E56DB1', alpha=0.5) # Plot 2024 smoothed deaths on the axis ax1.fill_between(yob_2024_smoothed.index, yob_2024_smoothed.values, color='#5F4B8B', alpha=0.5) # Plot the smoothed difference as vertical bars with inverted gradient colors on the axis ax1.bar(difference_by_yob_smoothed.index, difference_by_yob_smoothed.values, color=colors, alpha=0.9) # Add labels, title, and other elements to the axis ax1.set_xlabel('Year of Birth', fontsize=14) ax1.set_ylabel('Annual Deaths', fontsize=14) ax1.set_title('Year of Birth Among OD Decedents', fontsize=16) ax1.axhline(0, color='black', linewidth=0.9, linestyle='-') plt.tight_layout() # Save as editable PDF plt.savefig("adjusted_deaths_by_yob_without_irr.pdf", format="pdf") plt.show()

Zooming in on Gen Z

From here, the final annotated figure was created using Adobe Illustrator 2025, based on the PDF export of the plot

Plotting as age at death instead of generation as a double check on what that format does for inference

# Calculate the percent difference in deaths by yob between 2022 and 2024 (not smoothed) percent_difference_by_yob = 100 * (yob_2024 - yob_2022) / yob_2022 # Filter the percent difference to include only years of birth between 1950 and 2000 percent_difference_by_yob = percent_difference_by_yob[(percent_difference_by_yob.index >= 1950) & (percent_difference_by_yob.index <= 2000)] # Drop any NaN or infinite values from the percent difference series percent_difference_by_yob = percent_difference_by_yob.replace([np.inf, -np.inf], np.nan).dropna() # Normalize the percent differences for coloring norm = plt.Normalize(-100, 0) # Set normalization range from 0 to -100 colors = plt.cm.Blues(norm(percent_difference_by_yob.values)) # Use Blues colormap for shading # Create a plot with percent difference on a linear scale plt.figure(figsize=(14, 8)) # Overlay the percent difference as vertical bars with blue shading plt.bar(percent_difference_by_yob.index, percent_difference_by_yob.values, color=colors, alpha=0.9) # Add labels, title plt.xlabel('Year of Birth', fontsize=14) plt.ylabel('Percent Difference (%)', fontsize=14) plt.title('% Difference by Year of Birth (1950-2000) Comparing 2024 vs 2022', fontsize=16) plt.axhline(0, color='black', linewidth=0.9, linestyle='-') # Add year of birth labels to the top of the bars starting at -10% for index, value in percent_difference_by_yob.items(): if value <= -10: # Only label bars with values less than or equal to -10% plt.text(index, -10, f'{index}', ha='center', va='bottom', fontsize=8, rotation=90, alpha=0.99, color='white', fontweight='bold') # Add percent change as small black numbers at the end of the bars (integer display) plt.text(index, value - 2, f'{int(value)}%', ha='center', va='top', fontsize=8, color='black') # Set the vertical axis to include -100 plt.ylim(-100, 0) # Add grid lines at 5% intervals plt.yticks(range(-100, 5, 5)) # Set y-ticks at 5% intervals plt.grid(axis='y', linestyle='--', alpha=0.2) plt.tight_layout() plt.show()

Differences 2024 vs. 2022 by age decade

Same Data, Better Graphs

Note that these are adjusted estimates based on correcting for data suppression rules and pending autopsies (described above). Therefore the numbers in each row are estimates.

# Create a new column for 10-year age groups def categorize_age_group(age): try: age = int(age.split()[0]) # Extract the numeric part of the age return f"{(age // 10) * 10}-{(age // 10) * 10 + 9} years" except: return "< 10 years" # For '< 1 year' or invalid entries df_age['Age Group'] = df_age['Single-Year Ages'].apply(categorize_age_group) # Filter data for 2022 and 2024 data_2022 = df_age[df_age['Year'] == 2022] data_2024 = df_age[df_age['Year'] == 2024] # Group by Age Group and sum Deaths for each year deaths_2022 = data_2022.groupby('Age Group')['Deaths'].sum() deaths_2024 = data_2024.groupby('Age Group')['Deaths'].sum() # Combine the data into a single DataFrame age_group_comparison = pd.DataFrame({ 'Deaths_2022': deaths_2022, 'Deaths_2024': deaths_2024 }) # Fill NaN values with 0 (in case some age groups are missing in a year) age_group_comparison = age_group_comparison.fillna(0) # Calculate the difference age_group_comparison['Difference'] = age_group_comparison['Deaths_2024'] - age_group_comparison['Deaths_2022'] # Calculate the cumulative difference age_group_comparison['Cumulative Difference'] = age_group_comparison['Difference'].cumsum() # Calculate the percent difference age_group_comparison['Percent Difference'] = ( (age_group_comparison['Difference'] / age_group_comparison['Deaths_2022']) * 100 ).round(1) # Replace infinite or NaN percent differences with 0 (e.g., when Deaths_2022 is 0) age_group_comparison['Percent Difference'] = age_group_comparison['Percent Difference'].replace([float('inf'), -float('inf'), float('nan')], 0) age_group_comparison

Differences 2024 vs. 2023 by age decade

Note that these are adjusted estimates based on correcting for data suppression rules and pending autopsies (described above). Therefore the numbers in each row are estimates. Counts in the youngest decile and oldest 2 deciles (less than 500 deaths) are more likely to be influenced by random rounding error.

# Create a new column for 10-year age groups def categorize_age_group(age): try: age = int(age.split()[0]) # Extract the numeric part of the age return f"{(age // 10) * 10}-{(age // 10) * 10 + 9} years" except: return "< 10 years" # For '< 1 year' or invalid entries df_age['Age Group'] = df_age['Single-Year Ages'].apply(categorize_age_group) # Filter data for 2023 and 2024 data_2023 = df_age[df_age['Year'] == 2023] data_2024 = df_age[df_age['Year'] == 2024] # Group by Age Group and sum Deaths_adj for each year deaths_2023 = data_2023.groupby('Age Group')['Deaths'].sum() deaths_2024 = data_2024.groupby('Age Group')['Deaths'].sum() # Combine the data into a single DataFrame age_group_comparison = pd.DataFrame({ 'Deaths_2023': deaths_2023, 'Deaths_2024': deaths_2024 }) # Fill NaN values with 0 (in case some age groups are missing in a year) age_group_comparison = age_group_comparison.fillna(0) # Calculate the difference age_group_comparison['Difference'] = age_group_comparison['Deaths_2024'] - age_group_comparison['Deaths_2023'] # Calculate the cumulative difference age_group_comparison['Cumulative Difference'] = age_group_comparison['Difference'].cumsum() # Calculate the percent difference age_group_comparison['Percent Difference'] = ( (age_group_comparison['Difference'] / age_group_comparison['Deaths_2023']) * 100 ).round(1) # Replace infinite or NaN percent differences with 0 (e.g., when Deaths_2022 is 0) age_group_comparison['Percent Difference'] = age_group_comparison['Percent Difference'].replace([float('inf'), -float('inf'), float('nan')], 0) age_group_comparison

# Create a new column for 5-year age groups def categorize_age_group_5yr(age): try: if '<' in age: return '< 1 year' age = int(age.split()[0]) # Extract the numeric part of the age if age < 5: return '1-4 years' return f"{(age // 5) * 5}-{(age // 5) * 5 + 4} years" except: return "Unknown" df_age['Age Group 5yr'] = df_age['Single-Year Ages'].apply(categorize_age_group_5yr) # Filter data for 2022 and 2024 data_2022 = df_age[df_age['Year'] == 2022] data_2024 = df_age[df_age['Year'] == 2024] # Group by 5-Year Age Group and sum Deaths for each year deaths_2022_5yr = data_2022.groupby('Age Group 5yr')['Deaths'].sum() deaths_2024_5yr = data_2024.groupby('Age Group 5yr')['Deaths'].sum().apply(np.ceil) # Round 2024 deaths up to integer # Combine the data into a single DataFrame age_group_comparison_5yr = pd.DataFrame({ 'Deaths_2022': deaths_2022_5yr, 'Deaths_2024': deaths_2024_5yr }) # Replace missing values with 5 as the midpoint of the suppressed range age_group_comparison_5yr = age_group_comparison_5yr.fillna(5) # Calculate the difference age_group_comparison_5yr['Difference'] = age_group_comparison_5yr['Deaths_2024'] - age_group_comparison_5yr['Deaths_2022'] # Calculate the cumulative difference age_group_comparison_5yr['Cumulative Difference'] = age_group_comparison_5yr['Difference'].cumsum() # Calculate the percent difference age_group_comparison_5yr['Percent Difference'] = ( (age_group_comparison_5yr['Difference'] / age_group_comparison_5yr['Deaths_2022']) * 100 ).round(1) # Replace infinite or NaN percent differences with 0 (e.g., when Deaths_2022 is 0) age_group_comparison_5yr['Percent Difference'] = age_group_comparison_5yr['Percent Difference'].replace([float('inf'), -float('inf'), float('nan')], 0) # Sort the DataFrame by lifespan ages (numerically) def sort_age_group(age_group): if age_group == '< 1 year': return -1 # Assign a value for sorting '< 1 year' before others elif age_group == 'Unknown': return float('inf') # Assign a value for sorting 'Unknown' at the end else: return int(age_group.split('-')[0]) # Extract the starting age for sorting age_group_comparison_5yr = age_group_comparison_5yr.sort_index(key=lambda x: x.map(sort_age_group)) age_group_comparison_5yr

Proof Table - Categorizing the Continuous

# Create a new DataFrame 'catcon' with year of birth, age, and deaths catcon = data_2024[['yob', 'Numeric Age', 'Deaths']].copy() # Filter out rows where year of birth is 2024 or later catcon = catcon[catcon['yob'] < 2023] # Rename columns for clarity catcon.columns = ['Year of Birth', 'Age at Death in 2024', 'Deaths 2024'] # Add a new column 'Age in 2022' by subtracting 2 from 'Age at Death in 2024' catcon['Age in 2022'] = catcon['Age at Death in 2024'] - 2 # Round up deaths to the nearest integer, except if Deaths are between 5.0 and 5.999999 to maintain identity of backfilled for suppression rules catcon['Deaths 2024'] = catcon['Deaths 2024'].apply(lambda x: int(np.ceil(x)) if x < 5.0 or x >= 6.0 else int(x)) # Merge in Deaths from 2022 by year of birth data_2022_grouped = data_2022.groupby('yob')['Deaths'].sum().reset_index() data_2022_grouped.columns = ['Year of Birth', 'Deaths 2022'] catcon = catcon.merge(data_2022_grouped, on='Year of Birth', how='left') # Replace NaN values in 'Deaths 2022' with 0 before converting to integer catcon['Deaths 2022'] = catcon['Deaths 2022'].fillna(0).apply(np.ceil).astype(int) # Add a new column for the difference in deaths between 2024 and 2022 catcon['Deaths Difference (2024-2022)'] = catcon['Deaths 2024'] - catcon['Deaths 2022'] # Define a function to categorize age into 5-year increments def categorize_age_5yr(age): if age < 0: return '<0' elif age < 5: return '1-4' else: return f"{(age // 5) * 5}-{(age // 5) * 5 + 4}" # Add new columns for Age Group in 2024 and Age Group in 2022 catcon['Age Group in 2024'] = catcon['Age at Death in 2024'].apply(categorize_age_5yr) catcon['Age Group in 2022'] = catcon['Age in 2022'].apply(categorize_age_5yr) # Display the DataFrame catcon

The implications of categorizing continuous age in 5-year increments obscures a birth-year effect. Between 2024 and 2022, OD deaths increased for those born from 2005 to 2011 (pink & red cells in Deaths Difference column). Kids born in 2008-2009 (red cells) would have been in age group 10-to-14 in 2022, but were 15 or 16 in 2024 at time of death, putting them in age group 15-to-19 (yellow cells).

Looking at the Deaths Difference column we can see the impact of the age-group boundary: An increase (+16) among those born in 2009 is swamped out by a large decrease (-175) among those born in 2003, as the yellow age-group boxes in the table shift downwards. Hence, older Gen Z seems to have adopted strongly protective behaviors against overdose, whereas we cannot say the same for younger Gen Z where ODs increased.

Put another way, putting people into 5-year bins while doing a 2 year comparison = When we use age-group comparisons over time, what we are actually saying is "What would be the difference in ODs if everyone stayed the same age between 2022 and 2024?" This is like measuring the depth of a river from a fixed dock, versus measuring from the deck of a boat moving down the river.

.css-15w88e5{color:var(--chakra-colors-fg-neutral-primary);font-weight:inherit;letter-spacing:-0.09px;}Generational Relevance of Recent Overdose Reductions