Conociendo nuestros datos de pingüinos. 🗺🧭🐧

Instalar librerías necesarias

Importar librerías

import empiricaldist import janitor import matplotlib.pyplot as plt import numpy as np import palmerpenguins import pandas as pd import scipy.stats import seaborn as sns import sklearn.metrics import statsmodels.api as sm import statsmodels.formula.api as smf import statsmodels.stats as ss import session_info

Run to view results

Establecer apariencia general de los gráficos

%matplotlib inline sns.set_style(style='whitegrid') sns.set_context(context='notebook') plt.rcParams['figure.figsize'] = (11, 9.4) penguin_color = { 'Adelie': '#ff6602ff', 'Gentoo': '#0f7175ff', 'Chinstrap': '#c65dc9ff' }

Run to view results

Cargar los datos

Utilizando el paquete palmerpenguins

Datos crudos

raw_penguins_df = palmerpenguins.load_penguins_raw() raw_penguins_df

Run to view results

Datos previamente procesados

preprocessed_penguins_df = palmerpenguins.load_penguins() preprocessed_penguins_df

Run to view results

Utilizando los conjuntos de datos de seaborn

preprocessed_penguins_df = sns.load_dataset("penguins")

Run to view results

Utilizando la interfaz de Deepnote

Links de importación de datos:

Conjunto de datos crudos.

Conjunto de datos previamente procesados.

raw_penguins_df2 = pd.read_csv('penguins_raw.csv') raw_penguins_df2

Run to view results

preprocessed_penguins_df2 = pd.read_csv('penguins.csv') preprocessed_penguins_df2

Run to view results

hasta acá se importó el dataframe

Colecta y validación de datos

¿Qué tipo de dato son las variables del conjunto de datos?

preprocessed_penguins_df.dtypes

Run to view results

¿Cuántas variables de cada tipo de dato tenemos en el conjunto de datos?

( preprocessed_penguins_df .dtypes .value_counts() )

Run to view results

¿Cuántas variables y observaciones tenemos en el conjunto de datos?

preprocessed_penguins_df.shape

Run to view results

¿Existen valores nulos explicitos en el conjunto de datos?

( preprocessed_penguins_df .isnull() # devuelve True si el valor es nulo / False si no .any() # ¿Hay valor nulo por variable? True = si )

Run to view results

De tener observaciones con valores nulos, ¿cuántas tenemos por cada variable?

( preprocessed_penguins_df .isnull() .sum() # cuantos valores nulos hay por variable .sort_values(ascending=False) # ordenar de mayor a menor )

Run to view results

¿Cuántos valores nulos tenemos en total en el conjunto de datos?

( preprocessed_penguins_df .isnull() .sum() # cuantos valores nulos hay por variable .sum() # total de valores nulos )

Run to view results

¿Cuál es la proporción de valores nulos por cada variable?

( preprocessed_penguins_df .isnull() # devuelve True si el valor es nulo / False si no .melt(value_name='missing') #transforma el dataframe en un dataframe de pares de variable y valor nulo. sI TIENE VALORES NULOS ONO )

Run to view results

( preprocessed_penguins_df .isnull() .melt(value_name='missing') .pipe( # pipe para aplicar una funcion. pasa el dataframe por una función lambda df: ( # lambda es una función anonima sns.displot( # displot es una función de seaborn para crear visualizaciones de tipo "barras apiladas" data=df, # dataframe y='variable',# variable hue='missing', # variable de agrupación multiple='fill', #rellenar los huecos aspect=2 # el ancho de la visualización ) ) ) )

Run to view results

¿Cómo podemos visualizar los valores nulos en todo el conjunto de datos?

( preprocessed_penguins_df .isnull() .transpose() # transponer el dataframe cambia el orden de las filas y columnas .pipe( lambda df: sns.heatmap(data=df) # heatmap es una función de seaborn para crear mapas de calor ) )

Run to view results

¿Cuántas observaciones perdemos si eliminamos los datos faltantes?

processed_penguins_df = ( preprocessed_penguins_df .dropna() # elimina las observaciones con valores nulos ) processed_penguins_df

Run to view results

Conteos y proporciones

Preludio: ¿Qué estadísticos describen el conjunto de datos?

Todas las variables

processed_penguins_df.describe(include='all') # all incluye todas las variables

Run to view results

Solo las numéricas

processed_penguins_df.describe(include=[np.number]) # np.number incluye solo las variables numéricas

Run to view results

Solo categóricas - 1

processed_penguins_df.describe(include=object) # object incluye solo las variables categóricas

Run to view results

Solo categóricas - 2

( processed_penguins_df .astype( # transforma los tipos de datos { 'species': 'category', # 'category' es una variable categórica 'island': 'category', 'sex': 'category' } ) .describe(include=['category', object]) )

Run to view results

¿Cómo visualizar los conteos?

Pandas

( processed_penguins_df .species # pregunto por la variable 'species' es una variable categórica .value_counts() # cuantos valores hay por cada categoría .plot( # plot es una función de pandas para crear visualizaciones kind='bar', # tipo de visualización # color=penguin_color.values() ) )

Run to view results

Seaborn

sns.catplot( # catplot es una función de seaborn para crear visualizaciones data=processed_penguins_df, x='species', kind='count',# tipo de visualización por conteo palette=penguin_color,# paleta de colores con la variable q definimos # order=processed_penguins_df.value_counts('species', sort=True).index )

Run to view results

#frecuencia de aparición de cada especie ( processed_penguins_df .value_counts('species', sort=True) # valores únicos por especie y conteos. sort=True ordena los valores de forma ascendente. index ordena los valores .reset_index(name='count') # reset_index crea un nuevo dataframe con las columnas 'species' y 'count' para q sns lo lea como una tabla. name cambia el nombre de la columna .pipe( # pipe para aplicar una función. pasa el dataframe por una función lambda df: ( # lambda es una función anonima, no tiene nombre. para graficar sns.barplot( # barplot es una función de seaborn para crear visualizaciones data=df, x='species', y='count', palette=penguin_color ) ) ) ) # sns hizo el conteo en el grafico anterior lo tuvimos q hacer nosotros

Run to view results

¿Cómo visualizar las proporciones?

( processed_penguins_df .add_column('variable', '') # agrega una columna vacía .pipe( lambda df: ( sns.displot( data=df, x='variable', hue='species', # que en una sola barrita q nos muestre todos los valores multiple='fill',#rellenar los huecos. si encuentra multiples apariciones q nos de la proporcion completa palette=penguin_color ) ) ) )

Run to view results

Medidas de tendencia central

Media o promedio

processed_penguins_df.bill_depth_mm.mean() # con pandas calcula la media de la variable bill_depth_mm del dataframe, luego la variable y por ultimo la funciÃ³n mean() np.mean(processed_penguins_df.bill_depth_mm) # con numpy calcula la media de la variable bill_depth_mm del dataframe. entre parenesis se pone el conjunto d edatos y la variable a analizar processed_penguins_df.mean() # con pandas calcula la media de todas las varibles numericas del dataframe processed_penguins_df.median() processed_penguins_df.mode() processed_penguins_df.describe(include=object)

Run to view results

np.mean(processed_penguins_df.bill_depth_mm)

Run to view results

processed_penguins_df.mean()

Run to view results

Mediana

processed_penguins_df.median()

Run to view results

Moda

processed_penguins_df.mode()

Run to view results

processed_penguins_df.describe(include=object) # solo las variables categóricas

Run to view results

Estadistica Descriptiva Aplicada

Promedio de una variable usando pandas

data_frame.variable.mean()

Promedio de una variable usando numpy

np.mean(data_frame.variable)

Promedio para todas las variables numericas de un df

data_frame.mean()

Si al utilizar la funcion mean() sobre todo el dataset python les eleva una advertencia, esto puedo deberse a que hay columnas que no son numericas, para evitar esta advertencia prueba con: data_frame.mean( numeric_only= 'True' )

Mediana para todas las variables numericas del df

data_frame.median()

La moda se puede obtener para las variables tanto categoricas como numericas del df

data_frame.mode()

Información estadísticas de las variables categóricas

preprocessed_penguins_df.describe(include='object')

Medidas de dispersión

q tan cerca o tan lejos estas tus datos en relacion a estas medidas de tendencia central (moda, mediana, media)? para eso eso usamos las medidas de dispersión: rango, rango intercuatilico, desviación estandar.

Una curtosis mayor a 0 indica que la mayoria de los datos estan muy concentrados alrededor de la media, lo cual indica que hay poca variabilidad en los datos, es decir, el rango es pequeño. Una curtosis negativa indica lo contrario, los datos estan alejados de la media, lo cual indica mucha variabilidad en los datos, su rango es amplio

¿Cuál es el valor máximo de las variables?

Para conocer el rango tengo que saber los valores máximos y mínimos

processed_penguins_df.max()

Run to view results

processed_penguins_df.max(numeric_only=True) # calcula el maximo solo para las variables numericas

Run to view results

¿Cuál es el valor mínimo de las variables?

processed_penguins_df.min()

Run to view results

¿Cuál es el rango de las variables?

processed_penguins_df.max(numeric_only=True) - processed_penguins_df.min(numeric_only=True) # calcula el rango de las variables (la diferencia entre el valor maximo y el minimo)

Run to view results

¿Cuál es la desviación estándar de las variables?

processed_penguins_df.std()

Run to view results

si a la media le sumo la desviación estandar (std) y a la media le resto std. ese rango entre los dos resultados me va a dar el 65% de los datos (en distribución normal)

¿Cuál es el rango intercuartílico?

la media s epuede alterar con los valores atípicos. En cambio con los rangos intercuartiles son muy robustos porque se basan en percentiles (partimos nuestros datos en partes iguales, entonces nos evitamos estos sesgos si tneemos valores atipiocs

processed_penguins_df.quantile(0.25) # el primer cuartil

Run to view results

processed_penguins_df.quantile(0.75) - processed_penguins_df.quantile(0.25) # el rango intercuartilico. la diferencia entre el primer cuartil y el tercer cuartil. es el lugar donde capturamos el 50% de los datos alrededor de la media (25% abajo, 25% arriba)

Run to view results

( processed_penguins_df .quantile(q=[0.75, 0.50, 0.25]) # cuartiles .transpose() # transpone el dataframe .rename_axis('metric') # cambia el nombre de la columna .reset_index() # reset_index crea un nuevo dataframe con las columnas 'metric' para q sns lo lea como una tabla. a .assign( # agrega una nueva columna iqr = lambda df: df[0.75] - df[0.25] # calcula el rango intercuartilico que va a ser el valor de la columna iqr ) )

Run to view results

¿Cómo puedo visualizar la distribución de una variable?

Histograma

vamos a ver el diagrama de frecuncia de nuestros datos

sns.histplot( data=processed_penguins_df, x='flipper_length_mm', ) plt.axvline( # dibuja una linea en el histograma x=processed_penguins_df.flipper_length_mm.mean(), # la media color='red', linestyle='dashed', linewidth=2 ) plt.axvline( x=processed_penguins_df.flipper_length_mm.median(), # la mediana color='blue', linestyle='dashed', linewidth=2 ) plt.axvline( x=processed_penguins_df.flipper_length_mm.mode().values[0], color='black', linestyle='dashed', linewidth=4 ) plt.axvline( x=processed_penguins_df.flipper_length_mm.quantile(0.25), color='yellow', linestyle='dashed', linewidth=2 ) plt.axvline( x=processed_penguins_df.flipper_length_mm.quantile(0.75), color='yellow', linestyle='dashed', linewidth=2 )

Run to view results

Diagrama de caja / boxplot

Otra forma d evisualizar estos estadísticos de una forma muy sencilla es con un boxplot

sns.boxplot( data=processed_penguins_df, x="flipper_length_mm" )# el codigo de abajo hace lo mismo

Run to view results

sns.boxplot( x=processed_penguins_df.flipper_length_mm, )

Run to view results

Limitaciones

def freedman_diaconis_bindwidth(x: pd.Series) -> float: # define la función que calcula el binwidth, toma el rango intercuartilico y trata de estimar cual deberia ser ese binwidth optimo """Find optimal bindwidth using Freedman-Diaconis rule.""" IQR = x.quantile(0.75) - x.quantile(0.25) N = x.size return 2 * IQR / N ** (1 / 3)

Run to view results

sns.histplot( data=processed_penguins_df, x='flipper_length_mm', binwidth=6.3 ) plt.axvline( x=processed_penguins_df.flipper_length_mm.mean(), color='red', linestyle='dashed', linewidth=2 ) plt.axvline( x=processed_penguins_df.flipper_length_mm.median(), color='blue', linestyle='dashed', linewidth=2 ) plt.axvline( x=processed_penguins_df.flipper_length_mm.mode().values[0], color='black', linestyle='dashed', linewidth=4 ) plt.axvline( x=processed_penguins_df.flipper_length_mm.quantile(0.25), color='yellow', linestyle='dashed', linewidth=2 ) plt.axvline( x=processed_penguins_df.flipper_length_mm.quantile(0.75), color='yellow', linestyle='dashed', linewidth=2 )

Run to view results

Distribuciones: PMFs, CDFs y PDFs

Funciones de probabilidad de masas (PMFs)

Utilizando seaborn

sns.histplot( data=processed_penguins_df, x='flipper_length_mm', binwidth=1, stat='probability' # por defecto es 'count' )

Run to view results

Utilizando empiricaldist

pmf_flipper_length_mm = empiricaldist.Pmf.from_seq( # calcula la probabilidad de cada valor processed_penguins_df.flipper_length_mm, # la variable normalize=True # si ponemos False nos da la probabilidad acumulada (la freuencia?) )

Run to view results

pmf_flipper_length_mm.bar() # dibuja la distribución de la probabilidad calculada arriba

Run to view results

pmf_flipper_length_mm(231) # calcula la probabilidad de que el valor sea 231

Run to view results

processed_penguins_df.flipper_length_mm.max() # valor maximo

Run to view results

Funciones empirícas de probabilidad acumulada (ECDFs)

Utilizando seaborn

sns.ecdfplot( # calcula la probabilidad acumulada data=processed_penguins_df, x="flipper_length_mm" )

Run to view results

Utilizando empiricaldist

cdf_flipper_length_mm = empiricaldist.Cdf.from_seq( # calcula la probabilidad acumulada de probabilidades processed_penguins_df.flipper_length_mm, normalize=True )

Run to view results

cdf_flipper_length_mm.plot() # dibuja la probabilidad acumulada q = 200 # Specify quantity p = cdf_flipper_length_mm.forward(q) # Calculate probability plt.vlines( x=q, ymin=0, ymax=p, color = 'black', linestyle='dashed' ) plt.hlines( y=p, xmin=pmf_flipper_length_mm.qs[0], xmax=q, color='black', linestyle='dashed' ) plt.plot(q, p, 'ro')

Run to view results

cdf_flipper_length_mm.step() p_1 = 0.25 # Specify probability p_2 = 0.75 ps = (0.25, 0.75) # IQR qs = cdf_flipper_length_mm.inverse(ps) # Calcula quantiles plt.vlines( x=qs, ymin=0, ymax=ps, color = 'black', linestyle='dashed' ) plt.hlines( y=ps, xmin=pmf_flipper_length_mm.qs[0], xmax=qs, color='black', linestyle='dashed' ) plt.scatter( x=qs, y=ps, color='red', zorder=2 )

Run to view results

Comparando distribuciones

sns.ecdfplot( # calcula la probabilidad acumulada data=processed_penguins_df, x='flipper_length_mm', hue='species', # agrupar por especies palette=penguin_color )

Run to view results

Funciones de densidad de probabilidad

sns.kdeplot( # calcula la probabilidad de que el valor se encuentre en este rango data=processed_penguins_df, x='flipper_length_mm', bw_method=0.1 # binwidth )

Run to view results

stats = processed_penguins_df.body_mass_g.describe() stats

Run to view results

np.random.seed(42) # fijamos la semilla de numeros aleatorios xs = np.linspace(stats['min'], stats['max']) # crea un array de valores ys = scipy.stats.norm(stats['mean'], stats['std']).cdf(xs) # calcula la probabilidad en una distribución normal plt.plot(xs, ys, color='black', linestyle='dashed') # dibuja la curva de una distribución normal empiricaldist.Cdf.from_seq( # calcula la probabilidad acumulada processed_penguins_df.body_mass_g, normalize=True ).plot() # dibuja la probabilidad acumulada de nuestro dataset

Run to view results

xs = np.linspace(stats['min']-1000, stats['max'] + 1000) ys = scipy.stats.norm(stats['mean'], stats['std']).pdf(xs) # calcula la probabilidad de densidad, no la probabilidad acumulada plt.plot(xs, ys, color='black', linestyle='dashed') sns.kdeplot( # dibuja la distribución data=processed_penguins_df, x='body_mass_g' )

Run to view results

Ley de los Grandes Números y Teorema del Límite Central

Ley de los Grandes Números

dice = empiricaldist.Pmf.from_seq([1, 2, 3, 4, 5, 6]) # calcula la probabilidad 1/6 dice.bar()

Run to view results

for sample_size in (1e2, 1e3, 1e4): # 1e2 = 100, 1e3 = 1000, 1e4 = 10000 cantidad de tiradas por evento sample_size = int(sample_size) values = dice.sample(sample_size) # calcula la muestra, todas las tiradadas de dados sample_pmf = empiricaldist.Pmf.from_seq(values) # calcula la probabilidad plt.figure(figsize=(5,5)) # define el tamanio de la imagen sample_pmf.bar() # dibuja la probabilidad plt.axhline(y=1/6, color = 'red', linestyle='dashed') # dibuja la media. la probabilidad (teorica) media es 1/6 = 0.1667 plt.ylim([0, 0.50]) # limita el eje y plt.title(f"Sample size: {sample_size}")

Run to view results

Teorema del límite central

processed_penguins_df.sex.value_counts(normalize=True) # calcula proporcion de cada sexo. La distribución es binomial

Run to view results

sex_numeric = processed_penguins_df.sex.replace(['Male', 'Female'], [1, 0]) # transforma el sexo en 0 y 1

Run to view results

number_samples = 1000 # numero de muestras sample_size=35 # tamanio de la muestra samples_df = pd.DataFrame() np.random.seed(42) for i in range(1, number_samples + 1): sex_numeric_sample = sex_numeric.sample(sample_size, replace=True).to_numpy() sample_name = f"sample_{i}" samples_df[sample_name] = sex_numeric_sample male_population_mean = samples_df.mean().mean() print(f"Estimated percentage of male penguins in population is: {male_population_mean * 100:.4f}%") #porcentaje de machos

Run to view results

sample_means_binomial = pd.DataFrame(samples_df.mean(), columns=['sample_mean']) # calcula la media sns.kdeplot(data=sample_means_binomial) # grafica funcion de densidad plt.axvline(x=sex_numeric.mean(), color='red', linestyle='dashed') # grafica la media

Run to view results

# vamos a explorar cual es el efecto de aumentar el tamanio de la muestra en la estimacion d enuestro valor final sample_size_experiment = pd.DataFrame( [[i, samples_df.iloc[:, 0:i].mean().mean().mean()] for i in range(1, number_samples + 1)], columns=['sample_size', 'estimated_mean'] )

Run to view results

sns.scatterplot( data=sample_size_experiment, x='sample_size', y='estimated_mean' ) plt.axhline( y=sex_numeric.mean(), color='red', linestyle='dashed' ) plt.ylim([sex_numeric.mean() - 0.20, sex_numeric.mean() + 0.20])

Run to view results

La media de las muetras tiende aproximadamente a una distribución normal. Al ir calculando y aumentando el tamaño de las muestras vimos que podiamos calcular y encontrar la proporcion de machos en la poblacion sin problema, tomando pequeños muestreos cada vez y calculando los promedios.

Estableciendo relaciones: Gráfica de puntos

sns.scatterplot( # grafica puntos data=processed_penguins_df, x='bill_length_mm', y='bill_depth_mm', alpha=1/2, # transparencia s=100 # tamanio de los puntos )

Run to view results

sns.displot( # grafica distribuciones. Histograma de frecuencia de 2 dimensiones data=processed_penguins_df, x='bill_length_mm', y='bill_depth_mm', rug=True # ver como se distribuyen nuestros datos de manera unica. esto nos va a crear una linea x observacion q va encontrando )

Run to view results

sns.displot( data=processed_penguins_df, x='bill_length_mm', y='bill_depth_mm', kind='kde', # tipo de grafica. Estimamos las densidades q obtenemos en nuestra poblacion rug=True )

Run to view results

#se pueden combinar varios gráficos (gráfico disperción de puntos e histograma) sns.jointplot( # grafica de dos dimensiones data=processed_penguins_df, x='bill_length_mm', y='bill_depth_mm', marginal_kws=dict(bins=25, fill=False) # distribuciones marginales, bins = 25, fill = False, deshabilita las barras )

Run to view results

Estableciendo relaciones: Gráficos de violín y boxplots

vamos a relacionar variable categorica y una numerica

sns.scatterplot( # grafica puntos data=processed_penguins_df, x='species', # variable discreta y='flipper_length_mm', # variable numerica continua hue='species', palette=penguin_color )

Run to view results

meterle ruido

sns.stripplot( # grafica puntos, pero con linea de dispersion data=processed_penguins_df, x='species', y='flipper_length_mm', palette=penguin_color )

Run to view results

boxplot para visualizar propiedades estadísitcas que tiene nuestro conjunto de datos para cada una de nuestras variables categóricas

ax = sns.boxplot( data=processed_penguins_df, x='flipper_length_mm', y='species', palette=penguin_color, whis=np.inf # para no mostrar outliers ) ax = sns.stripplot( # grafica puntos, pero con linea de dispersion data=processed_penguins_df, x='flipper_length_mm', y='species', color='.3' )

Run to view results

ax = sns.violinplot( data=processed_penguins_df, x='species', y='flipper_length_mm', color='.8' ) ax = sns.stripplot( # stirpplot grafica puntos data=processed_penguins_df, x='species', y='flipper_length_mm', palette=penguin_color )

Run to view results

sns.swarmplot( # grafica puntos pone un punto al lado del otro. No es lo mismo que el stripplot porque no pone una linea de dispersion data=processed_penguins_df, x='species', y='flipper_length_mm', hue='species', palette=penguin_color )

Run to view results

##Código de los gráficos #Grafico de puntos sns.scatterplot( data=dataFrame, x='variable_categorica', y='variable_numerica', hue='variable categorica', #agrega un calor distinto por categoria palette=nombre_paleta ) #Agrega ruido a los puntos para obtener una mejor visualizacion de como se distribuyen los datos sns.stripplot( data=dataFrame, x='variable_categorica', y='variable_numerica', palette=nombre_paleta ) #Grafico de boxplots mas grafico de puntos en un mismo grafico ax = sns.boxplot( data=dataFrame, x='variable_categorica', y='variable_numerica', palette=nombre_paleta ) #grafico de puntos ax = sns.stripplot( data=dataFrame, x='variable_categorica', y='variable_numerica', color = 'black' ) #Grafico de violin mas grafico de puntos en una misma grafica ax = sns.violinplot( data=dataFrame, x='variable_categorica', y='variable_numerica', color='.8' ) #Grafico de puntos ax = sns.stripplot( data=dataFrame, x='variable_categorica', y='variable_numerica', palette=nombre_paleta ) #Grafico de swarmplot. Muestra todos los puntos de los datos sns.swarmplot( data=dataFrame, x='variable_categorica', y='variable_numerica', palette=nombre_paleta )

Run to view results

Estableciendo relaciones: Matrices de correlación

Si desean profundizar sobre la definicion del coeficiente de correlacion, les recomiendo leer a partir de la pagina 147 de este libro (que fue uno de los libros guía para el curso): https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf

¿Existe una correlación lineal entre alguna de nuestras variables?

processed_penguins_df.corr() # método de correlación. para ver coeficientes de correlación entre variables.

Run to view results

¿Como puedo visualizar los coeficientes de correlación?

sns.heatmap( # grafica de calor data=processed_penguins_df.corr(), #data = esta variable recibe una matriz cmap=sns.diverging_palette(20, 230, as_cmap=True), # paleta de colores divergentes, 20 = rojo, 230 = azul. center=0, vmin=-1, vmax=1, linewidths=0.5, cbar_kws={"shrink": 0.5}, annot=True )

Run to view results

Año no está muy relacionado con las otras variables

sns.clustermap( # grafica de agrupamiento según el valor que tenga la matriz data=processed_penguins_df.corr(), cmap= sns.diverging_palette(20, 230, as_cmap=True), # 'BrBG' center=0, vmin=-1, vmax=1, linewidths=0.5, cbar_kws={"shrink": 0.5}, annot=True )

Run to view results

¿Cómo podría representar una variable categórica como numérica discreta?

ver si variable categorica está relacionada con numerica

processed_penguins_df = ( processed_penguins_df .assign( # crea una nueva variable numeric_sex=lambda df: df.sex.replace(['Female', 'Male'], [0, 1]) # 0 = female, 1 = male ) )

Run to view results

sns.clustermap( data=processed_penguins_df.corr(), cmap= sns.diverging_palette(20, 230, as_cmap=True), # 'BrBG' center=0, vmin=-1, vmax=1, linewidths=0.5, cbar_kws={"shrink": 0.5}, annot=True )

Run to view results

Coeficiente Pearson: como visualizarlo graficamente de manera efectiva para obtener insagt visuales para ayudarte a identificar si hay o no una correlación y que tan fuerte es

¿Cuál es una límitante de los coeficientes de correlación lineal?

Sólo nos ayuda a determinar la posible existencia de una correlación lineal, sin embargo, su ausencia no significa que no exista otro tipo de correlación

x = np.linspace(-100, 100, 100) # crea un arreglo de elementos aleatorios. -100 = inicio, 100 = fin, 100 = elementos y = x ** 2 y += np.random.normal(0, 1000, x.size) # agrega ruido, 0 = media, 1000 = desviación estandar, x.size = elementos. Distribución normal. sns.scatterplot(x=x, y=y) np.corrcoef(x, y) # coeficiente de correlación, nos devuelve un numero entre -1 y 1

Run to view results

x = np.linspace(-100, 100, 100) y = x ** 3 y += np.random.normal(0, 1000, x.size) sns.scatterplot(x=x, y=y) np.corrcoef(x, y)

Run to view results

sns.scatterplot( data=processed_penguins_df, x='bill_length_mm', # longitud pico y='bill_depth_mm' # ancho pico )

Run to view results

El coeficiente de correlación no nos habla del impacto de la relación. (Podemos tener coeficiente de correlacion mas alto que otro, pero no quiere decir que nos va a servir para predecir o par ahacer algo que no de impacto)

np.random.seed(42) x_1 = np.linspace(0, 100, 100) y_1 = 0.1 * x_1 + 3 + np.random.uniform(-2, 2, size=x_1.size) sns.scatterplot( x=x_1, y=y_1 ) x_2 = np.linspace(0, 100, 100) y_2 = 0.5 * x_2 + 1 + np.random.uniform(0, 60, size=x_2.size) sns.scatterplot( x=x_2, y=y_2 ) plt.legend(labels=['1', '2']) print(np.corrcoef(x_1, y_1)) print(np.corrcoef(x_2, y_2))

Run to view results

de correlacion no nos alcanza para ver la fuerza del efecto

Estableciendo relaciones: Análisis de regresión simple (para establecer la fuerza del efecto)

La regresión lineal es una técnica que nos ayuda a hacer comparaciones entre los puntos en el plano cartesiano. es decir, que para un valor de X existe un valor de Y, esto se empieza a graficar sobre el plano como un grafico de dispersión

para esos datos, hay que ajustar una linea recta que mejor los entienda, ósea el modelo trata de predecir el mejor ajuste para la linea recta en esos datos.

La función matemática correspondiente a este problema es Y=w0 + w1x

X es un valor que existe sobre el plano W0 es el punto que se esta cortando sobre el plano, es decir, cuando X = 0 cual es el salto que existe el punto de X = 0 y el plano en el eje Y. W1 es cuando se agrega un valor a la X cuanto salto sobre Y Básicamente esto se conoce como w0 el Intercepto y w1 la pendiente de la linea recta.

durante el ajuste del modelo de regresión lineal se conocen como los pesos del modelo, estos son los valores que va a estar intentando aprender el modelo para entender cual va a ser la mejor linea recta que se va a ajustar a los datos.

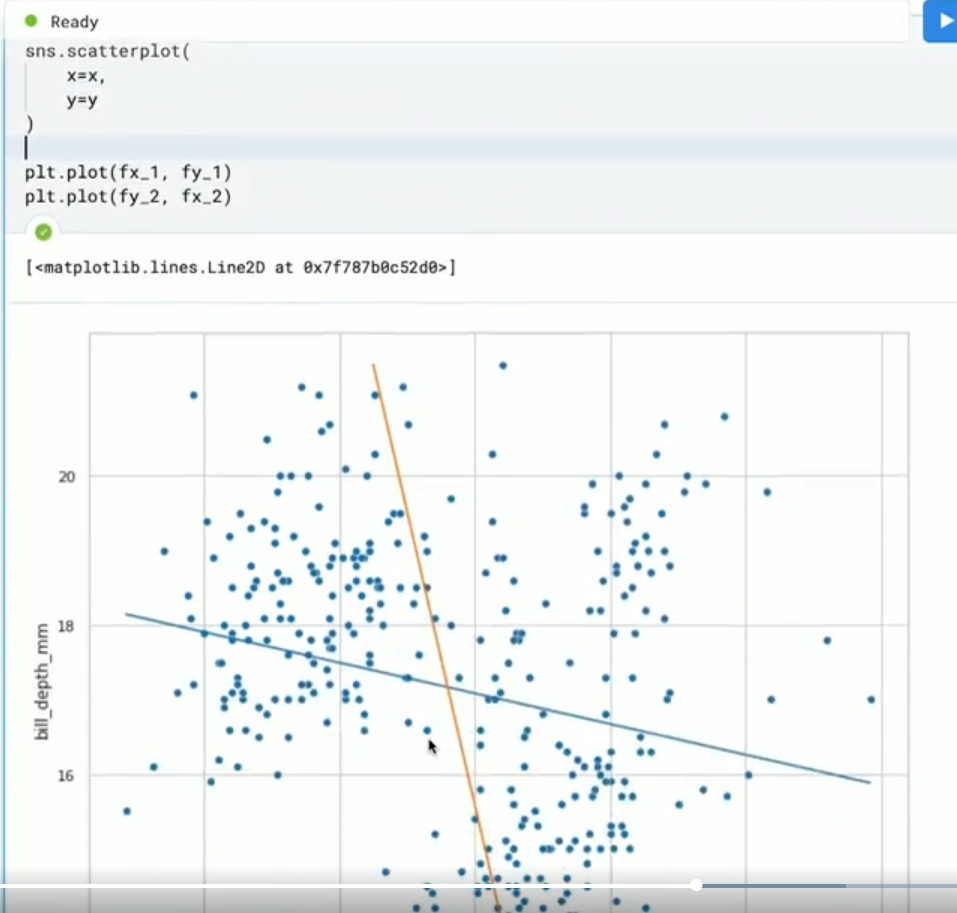
res_1 = scipy.stats.linregress(x=x_1, y=y_1) # coeficiente deregresión lineal res_2 = scipy.stats.linregress(x=x_2, y=y_2) print(res_1, res_2, sep="\n") # sep="\n" = salto de linea

Run to view results

slope = efecto que tiene esta correlación en caso de q exista. 0.1 estamos esperando un cambio muy pequeño cuando el cambio de x (azules)

slope = 0.54 mayor impacto en el conjunto de datos que estaban mas dispersos (naranja)

p_value = para saber si la correlación lineal es significativa

sns.scatterplot( x=x_1, y=y_1 ) fx_1 = np.array([x_1.min(), x_1.max()]) fy_1 = res_1.intercept + res_1.slope * fx_1 plt.plot(fx_1, fy_1) sns.scatterplot( x=x_2, y=y_2 ) fx_2 = np.array([x_2.min(), x_2.max()]) fy_2 = res_2.intercept + res_2.slope * fx_2 plt.plot(fx_2, fy_2) plt.legend(labels=['1', '1', '2', '2'])

Run to view results

sns.scatterplot( data=processed_penguins_df, x='bill_length_mm', y='bill_depth_mm' ) res_penguins = scipy.stats.linregress(x=processed_penguins_df.bill_length_mm, y=processed_penguins_df.bill_depth_mm) print(res_penguins) fx_1 = np.array([processed_penguins_df.bill_length_mm.min(), processed_penguins_df.bill_length_mm.max()]) fy_1 = res_penguins.intercept + res_penguins.slope * fx_1 plt.plot(fx_1, fy_1)

Run to view results

sns.lmplot( # Regresión lineal simple data=processed_penguins_df, x='bill_length_mm', y='bill_depth_mm', height=10 )

Run to view results

Limitaciones del análisis de regresión simple

La regresión lineal simple no es simétrica

x = processed_penguins_df.bill_length_mm y = processed_penguins_df.bill_depth_mm res_x_y = scipy.stats.linregress(x=x, y=y) # coeficiente de regresión lineal res_y_x = scipy.stats.linregress(y=x, x=y) print(res_x_y, res_y_x, sep="\n")

Run to view results

slope nos importa porque nos va a explicar como cambia una variable respecto a la otra

sns.scatterplot( x=x, y=y ) fx_1 = np.array([x.min(), x.max()]) fy_1 = res_x_y.intercept + res_x_y.slope * fx_1 plt.plot(fx_1, fy_1)

Run to view results

sns.scatterplot( x=y, y=x ) fx_1 = np.array([y.min(), y.max()]) fy_1 = res_y_x.intercept + res_y_x.slope * fx_1 plt.plot(fx_1, fy_1)

Run to view results

La regresión no nos dice nada sobre la causalidad, pero existen herramientas para separar las relaciones entre varias variables

La pendiente es -0.634905, lo que significa que cada milímetro adicional de profundidad del pico es asociado a un decremento de -0.634905 milímetros de la longitud del pico de un pingüino.

( smf.ols( # ols = Ordinary Least Squares, regresión lineal simple formula="bill_length_mm ~ bill_depth_mm", # bill_length_mm = Y, bill_depth_mm = X data=processed_penguins_df ) .fit() # .fit() = ajustar el modelo, .params # .params = para ver los valores de los coeficientes )

Run to view results

( smf.ols( formula="bill_depth_mm ~ bill_length_mm", data=processed_penguins_df ) .fit() .summary() )

Run to view results

Limitacion del Analisis de Regresion Simple La regresion lineal simple de A - B no es lo mismo que B - A. Las regresiones pueden ser diferentes en cada caso. Debes elegir de correctamente cual sera la variable independiente y dependiente.

Si dos variables crecen o decrecen siguiendo las mismas pautas, no implica necesariamente que una cause la otra. Correlacion no implica causalidad.

Solo puede manejar relaciones lineales. Es importante visualizar los datos para poder determinar que tipo de regression utilizar.

Análisis de regresión múltiple

El análisis de regresión múltiple es una técnica estadística utilizada para modelar la relación entre una variable de respuesta o dependiente y dos o más variables predictoras o independientes. A diferencia del análisis de regresión simple, que utiliza solo una variable predictora, el análisis de regresión múltiple permite analizar cómo dos o más variables predictoras influyen en la variable de respuesta. El objetivo del análisis de regresión múltiple es crear un modelo matemático que describa la relación entre las variables independientes y la variable dependiente. El modelo se utiliza para predecir los valores de la variable de respuesta en función de los valores de las variables predictoras. Además, el análisis de regresión múltiple puede ayudar a identificar qué variables predictoras son significativas para predecir la variable de respuesta. En el análisis de regresión múltiple, la variable dependiente debe ser continua, mientras que las variables predictoras pueden ser continuas o categóricas. Se utilizan diferentes técnicas estadísticas para ajustar el modelo de regresión múltiple y estimar los coeficientes de las variables predictoras.

Olvidé mi báscula para pesar a los pingüinos, ¿Cuál sería la mejor forma de capturar ese dato?

Creando modelos

model_1 = ( smf.ols( formula="body_mass_g ~ bill_length_mm", data=processed_penguins_df ) .fit() ) model_1.summary()

Run to view results

model_2 = ( smf.ols( formula="body_mass_g ~ bill_length_mm + bill_depth_mm ", data=processed_penguins_df ) .fit() ) model_2.summary()

Run to view results

model_3 = ( smf.ols( formula="body_mass_g ~ bill_length_mm + bill_depth_mm + flipper_length_mm", data=processed_penguins_df ) .fit() ) model_3.summary()

Run to view results

model_4 = ( smf.ols( formula="body_mass_g ~ bill_length_mm + bill_depth_mm + flipper_length_mm + C(sex)", data=processed_penguins_df ) .fit() ) model_4.summary()

Run to view results

model_5 = ( smf.ols( formula="body_mass_g ~ flipper_length_mm + C(sex)", data=processed_penguins_df ) .fit() ) model_5.summary()

Run to view results

Visualizando resultados

models_results = pd.DataFrame( dict( actual_value=processed_penguins_df.body_mass_g, prediction_model_1 = model_1.predict(), prediction_model_2 = model_2.predict(), prediction_model_3 = model_3.predict(), prediction_model_4 = model_4.predict(), prediction_model_5 = model_5.predict(), species=processed_penguins_df.species, sex=processed_penguins_df.sex ) ) models_results

Run to view results

sns.ecdfplot( data=models_results#.select_columns(['actual_value', 'prediction_model_5']) )

Run to view results

sns.kdeplot( data=models_results, cumulative=False )

Run to view results

sns.lmplot( data=processed_penguins_df, x='flipper_length_mm', y='body_mass_g', height=10, hue='sex' )

Run to view results

Análisis de regresión logística

smf.logit( formula='sex_numeric ~ flipper_length_mm + bill_length_mm + bill_depth_mm + C(island)', data=processed_penguins_df ).fit().summary()

Run to view results

( processed_penguins_df .value_counts(['island', 'sex', 'species']) .reset_index(name='count') )

Run to view results

processed_penguins_df.species.unique()

Run to view results

processed_penguins_df = ( processed_penguins_df .assign(is_adelie=lambda df: df.species.replace(['Adelie', 'Chinstrap', 'Gentoo'], [1, 0, 0])) )

Run to view results

model_is_adelie = smf.logit( formula='is_adelie ~ flipper_length_mm + C(sex)', data=processed_penguins_df ).fit(maxiter=100) model_is_adelie.params

Run to view results

is_adelie_df_predictions = pd.DataFrame( dict( actual_adelie = processed_penguins_df.species.replace(['Adelie', 'Chinstrap', 'Gentoo'], [1, 0, 0]), predicted_values = model_is_adelie.predict().round() ) ) is_adelie_df_predictions

Run to view results

( is_adelie_df_predictions .value_counts(['actual_adelie', 'predicted_values']) .reset_index(name='count') .pivot_wider( index='actual_adelie', names_from='predicted_values', values_from='count' ) .rename_column('actual_adelie', 'actual / predicted') )

Run to view results

print( sklearn.metrics.confusion_matrix( is_adelie_df_predictions.actual_adelie, is_adelie_df_predictions.predicted_values ) ) sklearn.metrics.accuracy_score( is_adelie_df_predictions.actual_adelie, is_adelie_df_predictions.predicted_values )

Run to view results

Jeinfferson Bernal G

Estudiante • hace 2 años Modelo para definir si un pinguino es Macho o Hembra

Creamos el modelo con las variables que consideremos influyen en la eleccion de si es un macho o hembra. Nuestra variable objetivo es categorica (sexo), por tanto, debemos convertirla en numerica para poder aplicar al modelo.

#Modelo logistico de la variable sexo VS longitud de las aletas, ancho del pico, largo del pico, y la isla smf.logit( formula='numeric_sex ~ flipper_length_mm + bill_length_mm + bill_depth_mm + C(island)', data=preprocessed_penguins_df ).fit().summary()

Run to view results

Dado que la variable sexo es categorica la convertimos en 0(hembras) y 1(machos), los resultados de la Regresion Logistica viene dado en funcion de los machos.

Los resultados se interpretan asi:

A mayor longitud de las aletas, mas probable que el pinguino sea macho (0.1393). A mayor longitud de los picos, mas probable que el pinguino sea macho (0.1413). Mientras mas ancho el pico, mas probable que sea macho (1.6401) Es menos probable que hayan machos en la isla Dream respecto a la Biscoe (-1.55) Es menos probable que hayan machos en la isla Torgensen respecto a la Biscoe (-1.03) El parametro P > abs(Z) indica cuales son las variables mas significativas estadisticamente para el resultado. Mientras mas tienda al valor 0 mas significativa es.

Cuando tenemos tres variables y en los resultados de la regresion logistica solo aparecen dos, indica que los esos valores son respecto a la variable faltante

Probabilidad de que hayan mas machos en la isla Dream que en la isla Torgensen

# Restamos los valores de probabilidad de cada isla -1.55 - (-1.03)

Run to view results

Respecto a la isla Dream, es mas probable encontrar macho en la isla Dream que en la Torgensen

Exploracion de las variables categoricas. Con un EDA inicial en las variables categoricas podriamos haber llegado a las misma conclusiones que el modelo logistico

#Tabla de conteo de las variables categoricas isla y sexo ( preprocessed_penguins_df .value_counts(['island', 'sex']) .reset_index(name='count') )

Paradoja de Simpson

Este video me ayudo a entender mejor la Paradoja de Simpson: https://www.youtube.com/watch?v=hpbXkrm68rI&ab_channel=MinutoDeFisica

Dejo más data por aquí: https://es.wikipedia.org/wiki/Paradoja_de_Simpson

sns.scatterplot( data=processed_penguins_df, x='bill_length_mm', y='bill_depth_mm' )

Run to view results

sns.regplot( data=processed_penguins_df, x='bill_length_mm', y='bill_depth_mm' )

Run to view results

sns.lmplot( data=processed_penguins_df, x='bill_length_mm', y='bill_depth_mm', hue='species', height=10, palette=penguin_color )

Run to view results

sns.pairplot(data=processed_penguins_df, hue='species', palette=penguin_color)

Run to view results

Que hacer cuando tengo muchas variables? Cuando se tiene muchas variables, un analisis de pares de variables puede ser confuso por lo que tenemos que recurrir a tecnicas que nos ayudan a entender la variacion de todos los datos de manera simple: Reduciendo las dimensiones para obtener un unico espacio (Pasar de 10 variables a solo 2). Algunas de estas tecnicas son:

Analisis de Componentes Principales (PCA): un ejemplo de utilidad es la demostracion de que los genes reflejan la geografia de Europa TSNE (T - Distributed Stochastic Neighbor Embedding): Separacion de todos los tipos de cancer UMAP (Uniform Manifold Approximation and Projection for Dimension Reduction): intenta capturar la estructura global preservando la estructura local de los datos utlizando proyecciones en un plano Comparacion: algoritmo de reduccion de dimension vs conjunto de datos

Información de sesión

session_info.show()

Run to view results