Metodo de Monte Carlo

Elaborado por: Guillermo Alvarez y Domenica Escobar

Introducción

El método Monte Carlo, que lleva el nombre del famoso Casino Monte Carlo de Mónaco, es un método estadístico que se ha convertido en una herramienta fundamental en diversos campos, desde la física hasta la ingeniería y la economía. Sus aplicaciones se extienden a una variedad de problemas que involucran procesos estocásticos y generación de números aleatorios.

En este ejercicio práctico, nos sumergiremos en el fascinante mundo de la integración numérica de Monte Carlo, centrándonos específicamente en dos enfoques clave: el método de muestreo (sampling) y el método "Hit and Miss" (aciertos y fallos).

Objetivos

Los cálculos integrales utilizan métodos de Monte Carlo para aproximar el valor de una integral particular. Para hacer esto, dividimos el intervalo integral en un número finito de subintervalos y calculamos el valor del integrando en un número aleatorio de puntos en cada subintervalo.

Este informe presenta experimentos computacionales en Python utilizando la tecnica de muestreo y de acierto de Monte Carlo. Estos métodos se utilizan para estimar integrales y resolver problemas de probabilidad.

Marco Teorico

El método Monte Carlo es un método numérico basado en experimentos aleatorios repetidos. Se utiliza para resolver problemas de difícil o imposible solución mediante técnicas analíticas.

El marco teórico del método Monte Carlo se basa en las siguientes ideas. Si un experimento aleatorio se repite suficientes veces, la frecuencia relativa con la que ocurre cada resultado es aproximadamente igual a la probabilidad de ese resultado.

Por ejemplo, si lanza una moneda 100 veces, la frecuencia relativa de cara, o la probabilidad de que salga cara, es aproximadamente la mitad.

En estadística, el método de Monte Carlo se utiliza para generar muestras y poblaciones aleatorias. Para ello se genera un conjunto de números aleatorios según la distribución de la población.

Los métodos de Monte Carlo se pueden utilizar para generar muestras aleatorias a partir de diversas distribuciones, que incluyen:

Distribución discreta

Distribución continua

Distribución multimodal

Ventajas y desventajas del método Monte Carlo

El método Monte Carlo tiene muchas ventajas, entre ellas:

Puede utilizarse para resolver problemas difíciles o imposibles de resolver utilizando técnicas analíticas.

Un método general que se puede aplicar a una variedad de problemas.

Este es un método flexible que se puede adaptar a diferentes escenarios.

Sin embargo, el método Monte Carlo también tiene algunos inconvenientes:

La precisión de la aproximación depende del número de puntos aleatorios utilizados.

Este puede ser un método costoso en términos de tiempo de ejecución.

Problema a resolver

El diagrama a resolver es un cuadrado con cuatro cuartos de círculo en su interior. La longitud de un lado de un cuadrado es 4 y el radio de un círculo es 1.

El área del cuadrado es 4 * 4 = 16.

El área de cada cuarto de círculo es π * 1^2 / 4 = π / 4.

El área del área sombreada es 16 - 4 * π / 4 = 16 - π.

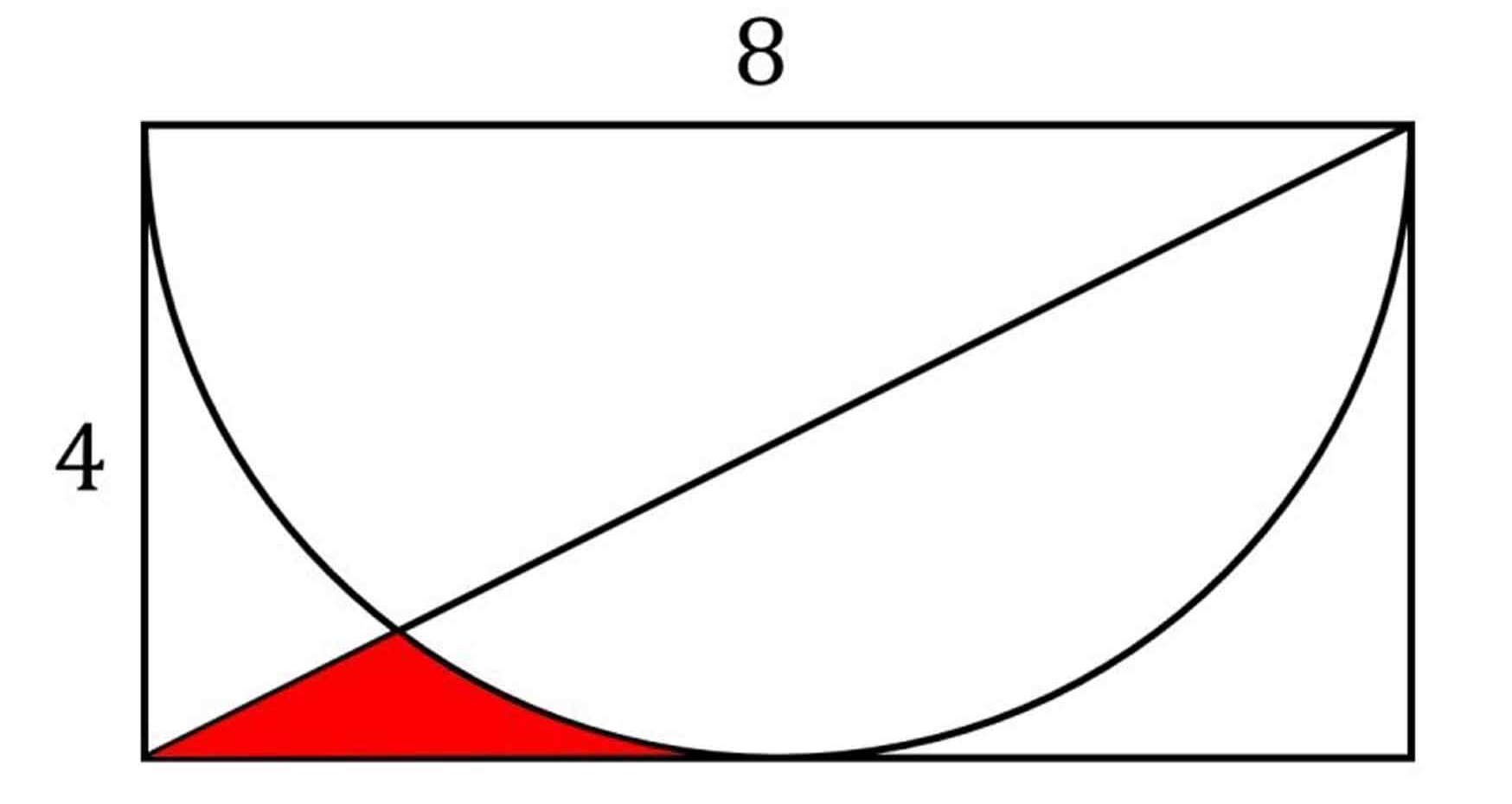
Gracias a la representacion gráfica se puede ver mas facilmente lo que buscamos resolver mediante el metodo de Monte Carlo

Métodos a utilizar

Metodo de muestreo(sampling)

En general, el método de Monte Carlo es un método de cálculo numérico que se basa en la generación de números aleatorios. Se utiliza para resolver problemas que son difíciles o imposibles de resolver mediante métodos analíticos. Este se basa en la siguiente idea:

Es la generación de puntos aleatorios dentro de un dominio específico para aproximar una solución numérica a un problema dado

Para tener una idea mas clara, si nosotros lanzamos una moneda al aire 100 veces, la frecuencia relativa con la que salga cara se aproximará a 1/2, que es la probabilidad de que salga cara.

Dentro del método de Monte Carlo, se utiliza esta idea para estimar valores o probabilidades. Esto se hace generando una gran cantidad de puntos aleatorios y calculando el valor o probabilidad de la función que desea estimar en cada punto. de manera en que el valor estimado se obtiene calculando el promedio de los valores obtenidos en puntos aleatorios y en cuantos más puntos aleatorios se generen, más mucho mas precisa será la estimación. De esta manera los métodos de Monte Carlo se pueden utilizar para resolver una gran cantidad de problemas, los cuales incluyen a los siguientes:

Cálculos integrales

Simulación de sistemas estocásticos

Optimización

Estadísticas

Ventajas del método Monte Carlo

El método Monte Carlo tiene una gran cantidad de ventajas, entre ellas:

Puede utilizarse para resolver problemas difíciles o imposibles de resolver utilizando técnicas analíticas.

Un método general que se puede aplicar a una variedad de problemas.

Este es un método flexible que se puede adaptar a diferentes escenarios.

Desventajas del método Monte Carlo

La precisión de la aproximación depende del número de puntos aleatorios utilizados.

Este puede ser un método costoso en términos de tiempo de ejecución.

La precisión de la aproximación puede verse afectada por la calidad de los números aleatorios generados.

Metodo de hit and miss

"Acertar y fallar" o Hit and Miss es un tipo de estimación del área de una región o de cálculo de la integral de una función. A diferencia de los métodos de muestreo, en el método de acierto y error, los puntos aleatorios no se generan dentro de un dominio específico, sino dentro de un dominio más amplio que incluye la región de interés. Luego se verifica cada punto para ver si "llega" a la región de interés, y esta información se utiliza para calcular la estimación.

El método de hit and miss tiene varias ventajas, donde se incluye:

Es un método simple y fácil de implementar.

Es un método general que se puede aplicar a una variedad de problemas.

El método de hit and miss también tiene algunas desventajas, incluyendo:

Y de igual manera tiene algunas desventajas:

La precisión de la aproximación depende del número de puntos aleatorios que se utilicen.

Puede ser un método costoso en términos de tiempo de ejecución.

Solucion

Para generar la solucion de este ejercicio debemos de ir desde lo mas sencillo hasta lo mas complicado, de manera en que logremos tener una vision mas real del ejercicio, para ello empezaremos realizando un modelo computacional de lo que pudimos ver anteriormente

Run to view results

Entonces, para comprender de mejor manera el codigo tendremos que aclarar lo siguiente:

"X" y "Y" se definen como arreglos espaciados linealmente entre 0 y 8 para x y entre 0 y 4 para y. Estos rangos representan los valores a lo largo de los ejes x e y dentro de el gráfico.

Creación de Malla:

"np.meshgrid" es una funcion de la libreria que importamos al inicio del codigo llamada "NumPy" se utiliza para crear una malla bidimensional (X e Y) a partir de los arreglos x e y. Esta malla será utilizada para evaluar las funciones en cada punto. Ahora para definir las funcione, lo hacemos de la siguiente manera: Definiremos F1 y F2 en términos de X e Y. Estas funciones representan las ecuaciones de contorno que se quieren graficar. Creación de la Figura y los Ejes:

Gracias a eso podemos definir de manera computacional el grafico que teniamos anteriormente y podemos encontrar un alto similar entre ellos

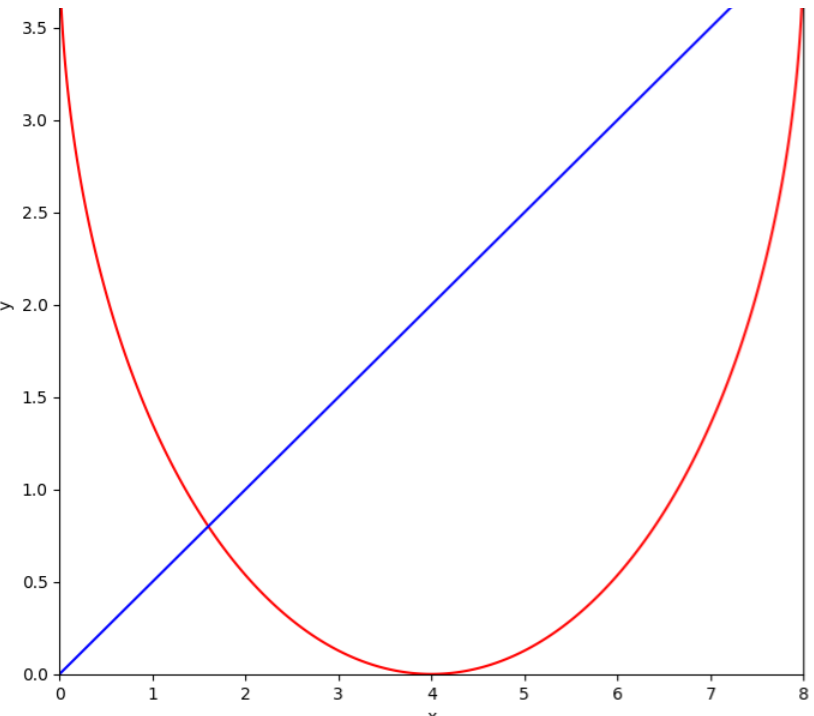
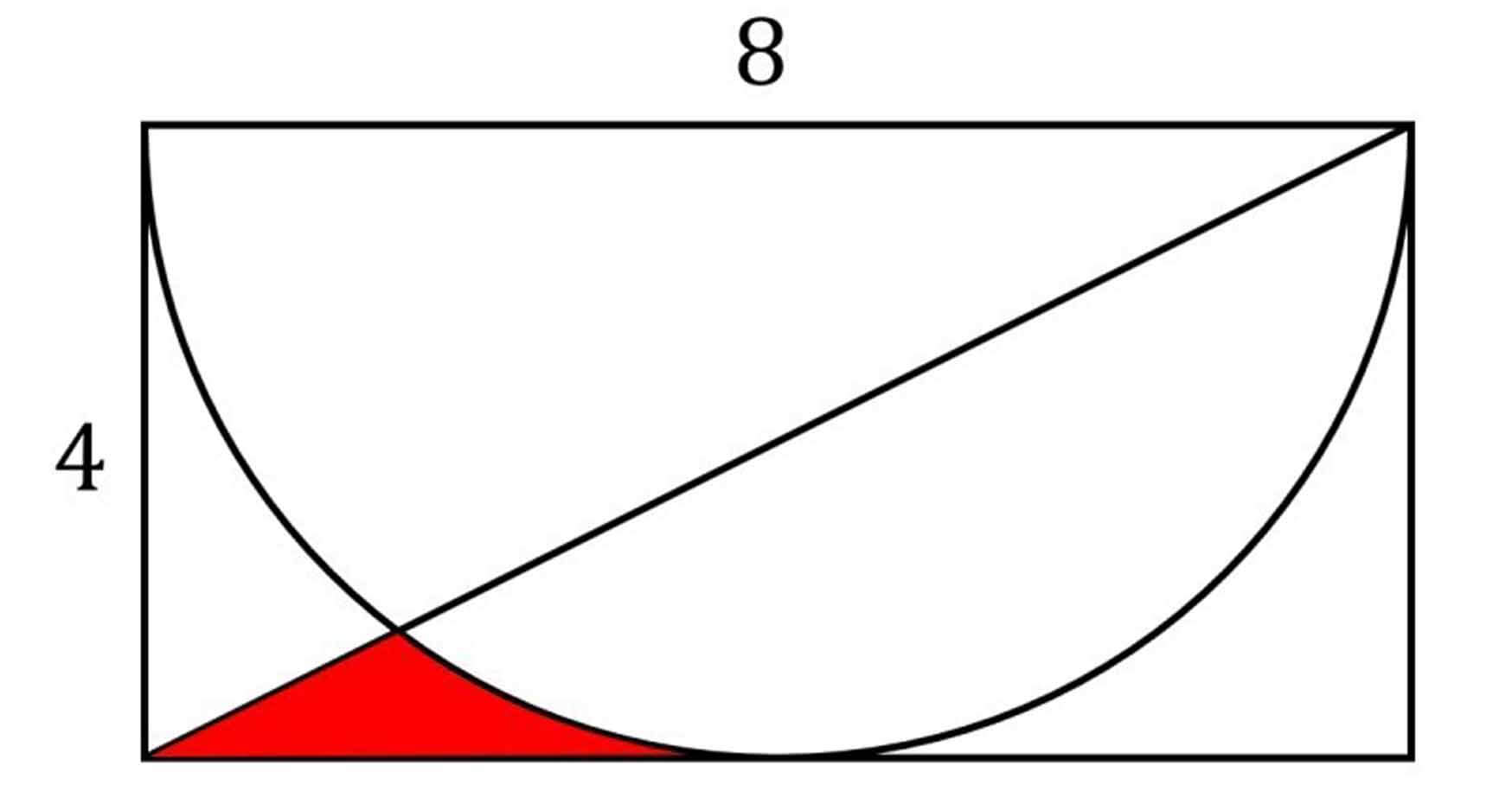
Una vez que realizamos la figura, ahora falta econtrar la manera de aislar y tener en cuenta solamente el area sombreada

# Importación de bibliotecas import matplotlib.pyplot as plt import numpy as np # Definición del rango de valores para x y y x = np.linspace(0, 8, 400) y = np.linspace(0, 4, 400) # Creación de una malla de coordenadas X, Y = np.meshgrid(x, y) # Definición de las funciones F1 = (X-4)**2 + (Y-4)**2 - 4**2 F2 = Y - 0.5 * X # Creación de la figura y los ejes plt.figure(figsize=(8, 4)) ax = plt.gca() # Dibujo de las funciones dentro de los dominios especificados circle_contour = ax.contour(X, Y, F1, levels=[0], colors='k') line_contour = ax.contour(X, Y, F2, levels=[0], colors='k') # Rellenar el área bajo la curva en el dominio especificado # Primero, necesitamos encontrar los puntos de intersección interseccion_x = [4 - np.sqrt(16 - y**2) for y in x if y <= 4 and (4 - np.sqrt(16 - y**2)) >= 0] interseccion_y = [y for y in x if y <= 4 and (4 - np.sqrt(16 - y**2)) >= 0] area_x = np.linspace(0, min(interseccion_x), 400) area_y = 0.5 * area_x ax.fill_between(area_x, 0, area_y, color='red') # Configuración de los límites de los ejes ax.set_xlim([0, 8]) ax.set_ylim([0, 4]) # Etiquetas y título ax.set_xlabel('x') ax.set_ylabel('y') ax.set_title('Gráfico de la Función con Área Sombreada') # Mostrar el gráfico plt.show()

Run to view results

Dentro de este nuevo grafico realizamos una acciones nuevas

Rellenar el Área Bajo la Curva: La misma que se encuentra la intersección de las funciones y se crea un área sombreada bajo la curva de la función F2 en el dominio especificado. Esta área está sombreada en rojo utilizando ax.fill_between. Resaltandola de la siguiente manera

import matplotlib.pyplot as plt import numpy as np # Definición del rango de valores para x y y x = np.linspace(0, 8, 400) y = np.linspace(0, 4, 400) # Creación de una malla de coordenadas X, Y = np.meshgrid(x, y) # Definición de las funciones F1 = (X-4)**2 + (Y-4)**2 - 4**2 F2 = Y - 0.5 * X # Creación de la figura y los ejes plt.figure(figsize=(8, 4)) ax = plt.gca() # Dibujo de las funciones dentro de los dominios especificados circle = ax.contour(X, Y, F1, levels=[0], colors='black') line = ax.contour(X, Y, F2, levels=[0], colors='black') # Relleno de la región de intersección # Para el relleno, necesitamos encontrar la intersección de las dos funciones. # Utilizaremos el método de malla para verificar dónde las dos funciones tienen un valor menor que cero. intersection = np.logical_and(F1 < 0, F2 < 0) ax.contourf(X, Y, intersection, 1, colors='red', alpha=0.5) # Configuración de los límites de los ejes ax.set_xlim([0, 8]) ax.set_ylim([0, 4]) # Etiquetas y título ax.set_xlabel('x') ax.set_ylabel('y') ax.set_title('Gráfico de la Función con Área de Intersección Resaltada') # Dibujo del rectángulo delimitador rectangle = plt.Rectangle((0,0), 8, 4, linewidth=1, edgecolor='black', facecolor='none') ax.add_patch(rectangle) # Etiquetas en los ejes ax.text(8, -0.3, '8', verticalalignment='bottom', horizontalalignment='right', fontsize=12, color='black') ax.text(-0.3, 4, '4', verticalalignment='top', horizontalalignment='left', fontsize=12, color='black') # Mostrar el gráfico plt.show()

Run to view results

Como podemos ver ya tenemos toda el area del ejercicio marcada, pero ahora necesitamos marcar el area especifica en el cual se va a trabajar, y eso lo realizamos de la siguiente manera

# Importación de bibliotecas import matplotlib.pyplot as plt import numpy as np # Definición del rango de valores para x y y x = np.linspace(0, 8, 400) y = np.linspace(0, 4, 400) # Creación de una malla de coordenadas X, Y = np.meshgrid(x, y) # Definición de las funciones F1 = (X-4)**2 + (Y-4)**2 - 4**2 F2 = Y - 0.5 * X # Creación de la figura y los ejes plt.figure(figsize=(8, 8)) ax = plt.gca() # Dibujo de las funciones dentro de los dominios especificados contour1 = ax.contour(X, Y, F1, levels=[0], colors='black') contour2 = ax.contour(X, Y, F2, levels=[0], colors='black') # Rellenar el área entre las funciones y las restricciones de dominio # Primero, encontramos las intersecciones de las funciones para saber dónde comenzar y terminar el relleno # Sabemos que el límite superior es y=4 y el límite inferior es y=0 # La intersección en x ocurre cuando y=4 y (x-4)^2=0, que es x=4 # Rellenamos entre la línea recta y y=0 desde x=0 hasta x=4 x_fill = np.linspace(0, 4, 400) y_fill = 0.5 * x_fill ax.fill_between(x_fill, 0, y_fill, color='red') # Rellenamos entre el círculo y y=4 desde x=4 hasta x=8 # Para encontrar los valores de y correspondientes al círculo, resolvemos para y en la ecuación del círculo y_circle = 4 + np.sqrt(4**2 - (x_fill-4)**2) ax.fill_between(x_fill, y_circle, 4, color='red', where=(x_fill>=4)) # Configuración de los límites de los ejes y las etiquetas ax.set_xlim([0, 8]) ax.set_ylim([0, 4]) ax.set_xticks([0, 8]) ax.set_yticks([0, 4]) ax.set_xticklabels(['0', '8']) ax.set_yticklabels(['0', '4']) # Mostrar el gráfico plt.show()

Run to view results

Una vez definida un area el cual vamos a calcular, debemos encontrar dos areas las cuales son el area debajo del circulo y el area debajo de la linea que atraviesa el circulo, para empezar con uno de los metodos que vamos a aplicar dentro de este informe

# Importación de bibliotecas import numpy as np import matplotlib.pyplot as plt from scipy import integrate # Definición del rango de valores para x y y x = np.linspace(0, 8, 400) y = np.linspace(0, 4, 400) # Creación de una malla de coordenadas X, Y = np.meshgrid(x, y) # Definición de las ecuaciones circle_eq = (X - 4)**2 + (Y - 4)**2 - 4**2 # Corregida la ecuación para un círculo line_eq = Y - 0.5 * X # Creación de la figura y los ejes fig, ax = plt.subplots(figsize=(8, 4)) # Dibujo de los contornos de las ecuaciones en el plano ax.contour(X, Y, circle_eq, levels=[0], colors='black') ax.contour(X, Y, line_eq, levels=[0], colors='black') # Cálculo del área bajo la línea desde x=0 hasta x=2 area_line, _ = integrate.quad(lambda x: 0.5 * x, 0, 2) # Cálculo del área bajo el círculo desde x=2 hasta x=4 area_circle, _ = integrate.quad(lambda x: 4 - np.sqrt(4**2 - (x - 4)**2), 2, 4) # Relleno del área debajo de la línea pero sobre el círculo solo para valores de x de 0 a 4 ax.fill_between(x, np.minimum(0.5 * x, 4), where=(x <= 4) & (x >= 0), color='red', alpha=0.5) # Relleno del área bajo el círculo desde x=2 hasta x=4 ax.fill_between(x, 0, where=(x >= 2) & (x <= 4), color='red', alpha=0.5) # Configuración de los límites de los ejes y las etiquetas ax.set_xlim(0, 8) ax.set_ylim(0, 4) ax.set_xticks([0, 4, 8]) ax.set_yticks([0, 4]) ax.set_xticklabels(['0', '4', '8']) ax.set_yticklabels(['0', '4']) # Mostrar el gráfico plt.show() # Imprimir las áreas calculadas print("Área bajo la línea desde x=0 hasta x=2:", area_line) print("Área bajo el círculo desde x=2 hasta x=4:", area_circle)

Run to view results

Una vez definido el area donde trabajaremos podemos comenzar con el primer metodo

Metodo de Hit and Miss

Como mencionamos anteriormente el metodo de Hit and Miss es diferencia de los métodos de muestreo, en el método de acierto y error, los puntos aleatorios no se generan dentro de un dominio específico, sino dentro de un dominio más amplio que incluye la región de interés.

Entonces para hacer esto, realizaremos de la siguiente manera:

# Importación de bibliotecas import numpy as np import matplotlib.pyplot as plt # Definir la función de la región de interés def f(x, y): return (y < 0.5 * x) and ((x - 4)**2 + (y - 4)**2 - 4**2 < 0) # Función para realizar una muestra def realizar_muestra(a, b, n): return np.random.uniform(a, b, n) # Método de Hit and Miss def hit_and_miss(a, b, c, n): x_dentro, y_dentro, x_fuera, y_fuera = [], [], [], [] for i in range(n): x_r = realizar_muestra(a, b, 1)[0] y_r = realizar_muestra(0, c, 1)[0] # Comparamos (x_r, y_r) con f(x, y) if f(x_r, y_r): x_dentro.append(x_r) y_dentro.append(y_r) else: x_fuera.append(x_r) y_fuera.append(y_r) return x_dentro, y_dentro, x_fuera, y_fuera # Parámetros (a, b, c) = (0, 8, 4) # Rango de x y y x = np.linspace(0, 8, 400) y = np.linspace(0, 4, 400) # Área del cuadrado area_cuadrado = (b - a) * c # Realizar el método de Hit and Miss para diferentes valores de n t_muestras = [10, 100, 1000] for t in t_muestras: puntos = hit_and_miss(a, b, c, t) area = len(puntos[0]) / t * area_cuadrado print("Área para n =", t, "es", area) # Graficar la función y los puntos generados fig, ax = plt.subplots(figsize=(8, 4)) # Aquí falta la definición de las funciones circle_eq y line_eq que se utilizan en la visualización # Debes definirlas antes de esta parte del código ax.contour(X, Y, circle_eq, levels=[0], colors='black') ax.contour(X, Y, line_eq, levels=[0], colors='black') ax.fill_between(x, np.minimum(0.5 * x, 4), where=(x <= 4) & (x >= 0), color='red', alpha=0.5) ax.fill_between(x, 0, where=(x >= 2) & (x <= 4), color='red', alpha=0.5) ax.plot(puntos[0], puntos[1], 'o', label='Puntos dentro') ax.plot(puntos[2], puntos[3], 'o', label='Puntos fuera') ax.legend() plt.show()

Run to view results

Dentro del codigo hacemos lo siguiente:

Definimos la Función de la Región de Interés: La función f(x, y) define la región de interés mediante una expresión booleana que evalúa si un punto (x, y) está dentro de la región.

Función para Realizar una Muestra: La función realizar_muestra(a, b, n) genera una muestra aleatoria de n puntos en el rango (a, b).

Método de Hit and Miss: La función hit_and_miss(a, b, c, n) implementa el método de Hit and Miss. Genera n puntos aleatorios y determina si están dentro de la región utilizando la función f(x, y).

Parámetros y Área del Cuadrado: Definimos los parámetros (a, b, c) y se calcula el área total del cuadrado que contiene la región de interés.

Realización del Método de Hit and Miss: Se realiza el método de Hit and Miss para diferentes cantidades de muestras (t_muestras). Se imprime el área estimada para cada cantidad de muestras.

Graficar la Función y los Puntos Generados: Se crea un gráfico que muestra las funciones (circle_eq y line_eq) y los puntos generados por el método de Hit and Miss. Los puntos dentro de la región

import numpy as np import matplotlib.pyplot as plt # Define la ecuación de la línea def line_eq(x): return 0.5 * x # Define la ecuación del semicírculo def semicircle_eq(x): return 4 - np.sqrt(4**2 - (x - 4)**2) # Función para verificar si un punto (x, y) está debajo de la línea o el semicírculo def below_curve(x, y): return y < line_eq(x) if x < 2 else y < semicircle_eq(x) # Función para generar muestras aleatorias def realizar_muestra(a, b, n): return np.random.uniform(a, b, n) # Método de Hit and Miss def hit_and_miss(a, b, c, n): x_dentro, y_dentro, x_fuera, y_fuera = [], [], [], [] for i in range(n): x_r = realizar_muestra(a, b, 1)[0] y_r = realizar_muestra(0, c, 1)[0] # Verificar si el punto está debajo de la curva if below_curve(x_r, y_r): x_dentro.append(x_r) y_dentro.append(y_r) else: x_fuera.append(x_r) y_fuera.append(y_r) return x_dentro, y_dentro, x_fuera, y_fuera # Parámetros (a, b, c) = (0, 4, 4) # Área del cuadrado area_cuadrado = (b - a) * c # Realizar el método de Hit and Miss para diferentes valores de n t_muestras = [10, 100, 100000] for t in t_muestras: puntos = hit_and_miss(a, b, c, t) area = len(puntos[0]) / t * area_cuadrado print("Área para n =", t, "es", area) # Graficar las funciones y los puntos generados x = np.linspace(0, 8, 400) y_line = line_eq(x) y_semicircle = np.piecewise(x, [x < 1.6, x >= 1.6], [lambda x: 0, semicircle_eq]) fig, ax = plt.subplots(figsize=(8, 4)) ax.plot(x, y_line, label='Línea') ax.plot(x, y_semicircle, label='Semicírculo') ax.fill_between(x, np.minimum(0.5 * x, 4), where=(x <= 4) & (x >= 0), color='red', alpha=0.5) ax.fill_between(x, 0, where=(x >= 1.6) & (x <= 4), color='red', alpha=0.5) ax.plot(puntos[0], puntos[1], 'o', label='Puntos dentro') ax.plot(puntos[2], puntos[3], 'o', label='Puntos fuera') ax.legend() plt.show()

Run to view results

Ahora implementamos una nueva funcion la cual nos ayuda a:

verificar si un Punto está Debajo de la Curva:

de la siguiente manera below_curve(x, y): Verifica si un punto (x, y) está debajo de la línea o el semicírculo, dependiendo de la ubicación en el eje x.

De igual manera tenemos una funcion para ejecutar diferentes iteraciones para Diferentes Valores de n:

t_muestras = [10, 100, 100000]: Define una lista de diferentes tamaños de muestra. Para cada valor en t_muestras, se ejecuta el método de Hit and Miss y se calcula el área utilizando los puntos generados. Imprime las áreas obtenidas para cada tamaño de muestra.

Con estas iteraciones es una herramienta para analizar cómo la variación en el tamaño de muestra afecta la precisión de la estimación del área bajo la curva utilizando el método de Hit and Miss. Permite entender cómo la cantidad de datos aleatorios afecta la calidad de la aproximación numérica del área deseada.

Entonces nosotros lo hacemos de la siguiente manera

1.-Lista de Tamaños de Muestra: t_muestras = [10, 100, 100000]: Definimos tres tamañosdiferentes. donde caada valor en esta lista representa cuántos puntos aleatorios se generarán para estimar el área.

2.-Iteración y Cálculo del Área: Para cada valor en t_muestras (por ejemplo, 10, 100, 100000): Se ejecuta el método de Hit and Miss (hit_and_miss(a, b, c, n)) con el tamaño de muestra actual de ( n). De esta manera los puntos generados aleatoriamente se usan para calcular el area bajo del circulo.

Entonces siempre debemos tomar en cuenta que la precisión de la estimación del área mejora a medida que aumenta el tamaño de muestra.

import numpy as np import matplotlib.pyplot as plt # Define the line equation def line_eq(x): return 0.5 * x # Define the semicircle equation def semicircle_eq(x): return 4 - np.sqrt(4**2 - (x - 4)**2) # Function to check if a point (x, y) is below the line or semicircle def below_curve(x, y): return y < line_eq(x) if x < 2 else y < semicircle_eq(x) # Function to generate random samples def realizar_muestra(a, b, n): return np.random.uniform(a, b, n) # Hit and miss method def hit_and_miss(a, b, c, n): x_dentro, y_dentro, x_fuera, y_fuera = [], [], [], [] for i in range(n): x_r = realizar_muestra(a, b, 1)[0] y_r = realizar_muestra(0, c, 1)[0] # Check if the point is below the curve if below_curve(x_r, y_r): x_dentro.append(x_r) y_dentro.append(y_r) else: x_fuera.append(x_r) y_fuera.append(y_r) return x_dentro, y_dentro, x_fuera, y_fuera # Parameters (a, b, c) = (0, 8, 4) # Square area area_cuadrado = (b - a) * c # Perform the hit and miss method for different values of n t_muestras = [10, 100, 1000] for t in t_muestras: puntos = hit_and_miss(a, b, c, t) area = len(puntos[0]) / t * area_cuadrado print("Área para n =", t, "es", area) # Plot the functions and the generated points x = np.linspace(0, 8, 400) y_line = line_eq(x) y_semicircle = np.piecewise(x, [x < 2, x >= 2], [lambda x: 0, semicircle_eq]) fig, ax = plt.subplots(figsize=(8, 4)) ax.plot(x, y_line, label='Linea') ax.plot(x, y_semicircle, label='Semicírculo') ax.fill_between(x, np.minimum(0.5 * x, 4), where=(x <= 4) & (x >= 0), color='red', alpha=0.5) ax.fill_between(x, 0, where=(x >= 2) & (x <= 4), color='red', alpha=0.5) ax.plot(puntos[0], puntos[1], 'o', label='Puntos dentro') ax.plot(puntos[2], puntos[3], 'o', label='Puntos fuera') ax.legend() plt.show()

Run to view results

Ahora buscaremos los puntos que se encuentran fuera de circulo

# Importar las bibliotecas necesarias import numpy as np import matplotlib.pyplot as plt # Definir la ecuación de la línea def line_eq(x): return 0.5 * x # Definir la ecuación del semicírculo def semicircle_eq(x): return 4 - np.sqrt(4**2 - (x - 4)**2) # Función para verificar si un punto (x, y) está debajo de la línea o el semicírculo def below_curve(x, y): return y < line_eq(x) if x <= 1.6 else y < semicircle_eq(x) # Función para generar muestras aleatorias def realizar_muestra(a, b, n): return np.random.uniform(a, b, n) # Método de Hit and Miss modificado def hit_and_miss(a, b, c, n): x_dentro, y_dentro, x_fuera, y_fuera = [], [], [], [] # Iterar para generar n puntos aleatorios for i in range(n): x_r = realizar_muestra(a, b, 1)[0] y_r = realizar_muestra(0, c, 1)[0] # Verificar si el punto está debajo de la curva if below_curve(x_r, y_r): x_dentro.append(x_r) y_dentro.append(y_r) else: x_fuera.append(x_r) y_fuera.append(y_r) return x_dentro, y_dentro, x_fuera, y_fuera # Parámetros (a, b, c) = (0, 6, 4) # Calcular el área del cuadrado area_cuadrado = (b - a) * c # Realizar el método de Hit and Miss para diferentes valores de n t_muestras = [10, 100, 1000] for t in t_muestras: # Obtener los puntos generados y calcular las áreas bajo la línea y el semicírculo puntos = hit_and_miss(a, b, c, t) area_linea = len([x for x in puntos[0] if x <= 1.6]) / t * area_cuadrado area_semicirculo = len([x for x in puntos[0] if x > 1.6]) / t * area_cuadrado # Imprimir las áreas calculadas print("Área bajo la línea para n =", t, "es", area_linea) print("Área bajo el semicírculo para n =", t, "es", area_semicirculo) # Generar valores para graficar las funciones x = np.linspace(0, 8, 400) y_linea = line_eq(x) y_semicirculo = np.piecewise(x, [x <= 1.6, x > 1.6], [line_eq, semicircle_eq]) # Crear la figura y los ejes para la visualización fig, ax = plt.subplots(figsize=(8, 4)) # Graficar la línea y el semicírculo ax.plot(x, y_linea, label='Línea') ax.plot(x, y_semicirculo, label='Semicírculo') # Rellenar las áreas bajo la línea y el semicírculo ax.fill_between(x, np.minimum(0.5 * x, 4), where=(x <= 1.6) & (x >= 0), color='red', alpha=0.5) ax.fill_between(x, 0, where=(x > 1.6) & (x <= 4), color='red', alpha=0.5) # Graficar los puntos generados dentro y fuera de la región ax.plot(puntos[0], puntos[1], 'o', label='Puntos dentro') ax.plot(puntos[2], puntos[3], 'o', label='Puntos fuera') # Mostrar la leyenda ax.legend() # Mostrar la visualización plt.show()

Run to view results

aqui implementamos un cambio a la funcion below_curve de manera en que below_curve(x, y): Verifica si un punto (x,y) está debajo de la línea o el semicírculo, dependiendo de la ubicación en el eje x. Gracias esto podemos saber si es que esta dentro de o fuera de la region sombreada que buscamos calcular

Para obtener el boceto final de la siguiente forma

# Importar las bibliotecas necesarias import numpy as np import matplotlib.pyplot as plt # Definir la ecuación de la línea def line_eq(x): return 0.5 * x # Definir la ecuación del semicírculo con límites actualizados def semicircle_eq(x): return np.where((x >= 1.6) & (x <= 4), 4 - np.sqrt(4**2 - (x - 4)**2), 0) # Función para verificar si un punto (x, y) está debajo de la línea o el semicírculo def below_curve(x, y): return y < line_eq(x) if x < 1.6 else y < semicircle_eq(x) # Función para generar muestras aleatorias def realizar_muestra(a, b, n): return np.random.uniform(a, b, n) # Método de Hit and Miss def hit_and_miss(a, b, c, n): x_dentro, y_dentro, x_fuera, y_fuera = [], [], [], [] # Iterar para generar n puntos aleatorios for i in range(n): x_r = realizar_muestra(a, b, 1)[0] y_r = realizar_muestra(0, c, 1)[0] # Verificar si el punto está debajo de la curva if below_curve(x_r, y_r): x_dentro.append(x_r) y_dentro.append(y_r) else: x_fuera.append(x_r) y_fuera.append(y_r) return x_dentro, y_dentro, x_fuera, y_fuera # Parámetros (a, b, c) = (0, 4, 4) # Calcular el área del cuadrado area_cuadrado = (b - a) * c # Realizar el método de Hit and Miss para diferentes valores de n t_muestras = [10, 100, 10000] for t in t_muestras: # Obtener los puntos generados y calcular el área puntos = hit_and_miss(a, b, c, t) area = len(puntos[0]) / t * area_cuadrado print("Área para n =", t, "es", area) # Generar valores para graficar las funciones x = np.linspace(0, 8, 400) y_linea = line_eq(x) y_semicirculo = np.piecewise(x, [x < 1.6, (x >= 1.6) & (x <= 4), x > 4], [lambda x: 0, semicircle_eq, lambda x: 0]) # Crear la figura y los ejes para la visualización fig, ax = plt.subplots(figsize=(8, 4)) # Graficar la línea y el semicírculo ax.plot(x, y_linea, label='Línea') ax.plot(x, y_semicirculo, label='Semicírculo') # Rellenar las áreas bajo la línea y el semicírculo ax.fill_between(x, np.minimum(0.5 * x, 4), where=(x <= 4) & (x >= 0), color='red', alpha=0.5) ax.fill_between(x, 0, where=(x >= 1.6) & (x <= 4), color='red', alpha=0.5) # Graficar los puntos generados dentro y fuera de la región ax.plot(puntos[0], puntos[1], 'o', label='Puntos dentro') ax.plot(puntos[2], puntos[3], 'o', label='Puntos fuera') # Mostrar la leyenda ax.legend() # Mostrar la visualización plt.show()

Run to view results

Metodo de Sampling

Como mencionamos en este informe el metodo de samplling , En general, el método de Monte Carlo es un método de cálculo numérico que se basa en la generación de números aleatorios. Se utiliza para resolver problemas que son difíciles o imposibles de resolver mediante métodos analíticos. Este se basa en la siguiente idea:

Es la generación de puntos aleatorios dentro de un dominio específico para aproximar una solución numérica a un problema dado

Entonces como ya hemos definido el area en el que vamos a trabajar este metodo se puede desarrollar de manera mas facil, y rapida, para ello lo realizamos de la siguiente

Dentro de este nuevo codigo podemos ver la siguiente funcion

def line_eq(x): return 0.5 * x

Run to view results

La misma que es utilizada para definir una linea mediante una funcion lineal, que en este caso es igual a y = 0.5 * x

Ahora mediante el siguiente codigo definimos el area del semicirculo de la siguiente manera

def semicircle_eq(x): return np.where((x >= 1.6) & (x <= 4), 4 - np.sqrt(4*2 - (x - 4)*2), 0)

Run to view results

De esta forma controlamos el area del semicirculo mediante un rango que esta entre 1.6 y 4., La ecuación del semicírculo está diseñada para representar la mitad superior de un círculo con un radio de 2

Ahora generamos nuevos datos dentro del rango

def realizar_muestra(a, b, n): return np.random.uniform(a, b, n)

Run to view results

Ahora crearemos la funcion de sampling la cual nos permitira la generacion de puntos de manera aleatorioa y su separacion entre puntos encima de la curva y puntos debajo de la curva

def sampling(a, b, c, n): # Generate random samples x_m = realizar_muestra(a, b, n) y_m = realizar_muestra(0, c, n) # Check if each point is below the curve below_curve_mask = np.all(np.vstack([y_m < line_eq(x_m), (x_m >= 1.6) & (y_m < semicircle_eq(x_m))]), axis=0) # Separate points below and above the curve x_dentro = x_m[below_curve_mask] y_dentro = y_m[below_curve_mask] x_fuera = x_m[~below_curve_mask] y_fuera = y_m[~below_curve_mask] return x_dentro, y_dentro, x_fuera, y_fuera

Run to view results

Esta region se vera representada por el area del cuadrado

area_cuadrado = (b - a) * c

Run to view results

Una vez que tenemos todo, solo faltara ejecutar el codigo y ver el resultado

# Realiza el método de muestreo para diferentes valores de n t_muestras = [10, 100, 10000] for t in t_muestras: puntos = sampling(a, b, c, t) area = len(puntos[0]) / t * area_cuadrado print("Área para n =", t, "es", area) # Grafica las funciones y los puntos generados x = np.linspace(0, 8, 400) y_line = line_eq(x) y_semicircle = np.piecewise(x, [x < 1.6, (x >= 1.6) & (x <= 4), x > 4], [lambda x: 0, semicircle_eq, lambda x: 0]) fig, ax = plt.subplots(figsize=(8, 4)) ax.plot(x, y_line, label='Línea') ax.plot(x, y_semicircle, label='Semicírculo') ax.fill_between(x, np.minimum(0.5 * x, 4), where=(x <= 4) & (x >= 0), color='red', alpha=0.5) ax.fill_between(x, 0, where=(x >= 1.6) & (x <= 4), color='red', alpha=0.5) ax.plot(puntos[0], puntos[1], 'o', label='Puntos dentro') ax.plot(puntos[2], puntos[3], 'o', label='Puntos fuera') ax.legend() plt.show()

Run to view results

Como podemos ver en el resultado, el area no se asemeja al area del ejercicio por ende es necesario realizar mas pruebas y simulaciones, ahora lo que intentaremos hacer es encontrar los puntos que se encuentran fuera tanto del semicirculo como de la linea recta de la siguiente manera

import numpy as np import matplotlib.pyplot as plt # Define la ecuación de la recta def line_eq(x): return 0.5 * x # Define la ecuación del semicírculo con límites actualizados def semicircle_eq(x): return np.where((x >= 1.6) & (x <= 4), 4 - np.sqrt(4*2 - (x - 4)*2), 0) # Función para verificar si un punto (x, y) está debajo de la recta def below_curve_recta(x, y): return y < line_eq(x) if x < 1.6 else False # Función para verificar si un punto (x, y) está debajo del semicírculo def below_curve_semicirculo(x, y): return y < semicircle_eq(x) if (x >= 1.6) and (x <= 4) else False # Función para generar muestras aleatorias def realizar_muestra(a, b, n): return np.random.uniform(a, b, n) # Método de muestreo def sampling(a, b, c, n): x_m = realizar_muestra(a, b, n) y_m = realizar_muestra(0, c, n) # Verifica si cada punto está debajo de la recta below_curve_recta_mask = np.all(np.vstack([y_m < line_eq(x_m), x_m < 1.6]), axis=0) # Verifica si cada punto está debajo del semicírculo below_curve_semicirculo_mask = np.all(np.vstack([y_m < semicircle_eq(x_m), (x_m >= 1.6) & (x_m <= 4)]), axis=0) # Separa los puntos debajo de la recta y el semicírculo, y los puntos fuera de ambas áreas x_dentro_recta = x_m[below_curve_recta_mask] y_dentro_recta = y_m[below_curve_recta_mask] x_dentro_semicirculo = x_m[below_curve_semicirculo_mask] y_dentro_semicirculo = y_m[below_curve_semicirculo_mask] x_fuera = x_m[~(below_curve_recta_mask | below_curve_semicirculo_mask)] y_fuera = y_m[~(below_curve_recta_mask | below_curve_semicirculo_mask)] return x_dentro_recta, y_dentro_recta, x_dentro_semicirculo, y_dentro_semicirculo, x_fuera, y_fuera # Parámetros (a, b, c) = (0, 4, 4) # Área del cuadrado area_cuadrado = (b - a) * c # Realiza el método de muestreo para diferentes valores de n t_muestras = [10, 100, 10000] for t in t_muestras: puntos = sampling(a, b, c, t) area_recta = len(puntos[0]) / t * area_cuadrado area_semicirculo = len(puntos[2]) / t * area_cuadrado print("Área para n =", t, "debajo de la recta es", area_recta) print("Área para n =", t, "debajo del semicírculo es", area_semicirculo) # Grafica las funciones y los puntos generados x = np.linspace(0, 8, 400) y_line = line_eq(x) y_semicircle = np.piecewise(x, [x < 1.6, (x >= 1.6) & (x <= 4), x > 4], [lambda x: 0, semicircle_eq, lambda x: 0]) fig, ax = plt.subplots(figsize=(8, 4)) ax.plot(x, y_line, label='Recta') ax.plot(x, y_semicircle, label='Semicírculo') ax.fill_between(x, np.minimum(0.5 * x, 4), where=(x <= 1.6) & (x >= 0), color='red', alpha=0.5, label='Área bajo la recta') ax.fill_between(x, 0, where=(x >= 1.6) & (x <= 4), color='blue', alpha=0.5, label='Área bajo el semicírculo') ax.plot(puntos[0], puntos[1], 'o', label='Puntos dentro de la recta') ax.plot(puntos[2], puntos[3], 'o', label='Puntos dentro del semicírculo') ax.plot(puntos[4], puntos[5], 'o', label='Puntos fuera de ambas áreas') ax.legend() plt.show()

Run to view results

Agregaremos una nuevas funciones las mismas que verifican si un punto está debajo de la recta o del semicírculo, respectivamente., y ademas, hemos ajustado la función de sampling para separar los puntos que están debajo de la recta y del semicírculo.

Una vez completado esto, debemos tomar en cuenta solo los puntos que se encuentran en la region que deseamos

import numpy as np import matplotlib.pyplot as plt # Define la ecuación de la línea def line_eq(x): return 0.5 * x # Define la ecuación del semicírculo con límites actualizados def semicircle_eq(x): return np.where((x >= 1.6) & (x <= 4), 4 - np.sqrt(4**2 - (x - 4)**2), 0) # Función para verificar si un punto (x, y) está debajo de la línea o el semicírculo def below_curves(x, y): if x < 1.6: return y < line_eq(x) else: return y < semicircle_eq(x) # Función para generar muestras aleatorias def realizar_muestra(a, b, n): return np.random.uniform(a, b, n) # Método de muestreo def sampling(a, b, c, n): x_m = realizar_muestra(a, b, n) y_m = realizar_muestra(0, c, n) # Verifica si cada punto está debajo de la curva below_curve_mask = np.array([below_curves(x, y) for x, y in zip(x_m, y_m)]) # Separa los puntos debajo y encima de la curva x_dentro = x_m[below_curve_mask] y_dentro = y_m[below_curve_mask] x_fuera = x_m[~below_curve_mask] y_fuera = y_m[~below_curve_mask] return x_dentro, y_dentro, x_fuera, y_fuera # Parámetros (a, b, c) = (0, 4, 4) # Área del cuadrado area_cuadrado = (b - a) * c # Realiza el método de muestreo para diferentes valores de n t_muestras = [10, 100, 10000] for t in t_muestras: puntos = sampling(a, b, c, t) area = len(puntos[0]) / t * area_cuadrado print("Área para n =", t, "es", area) # Grafica las funciones y los puntos generados x = np.linspace(0, 8, 400) y_line = line_eq(x) y_semicircle = np.piecewise(x, [x < 1.6, (x >= 1.6) & (x <= 4), x > 4], [lambda x: 0, semicircle_eq, lambda x: 0]) fig, ax = plt.subplots(figsize=(8, 4)) ax.plot(x, y_line, label='Línea') ax.plot(x, y_semicircle, label='Semicírculo') ax.fill_between(x, np.minimum(0.5 * x, 4), where=(x <= 4) & (x >= 0), color='red', alpha=0.5, label='Área bajo la recta') ax.fill_between(x, 0, where=(x >= 1.6) & (x <= 4), color='red', alpha=0.5, label='Área bajo el semicírculo') ax.plot(puntos[0], puntos[1], 'o', label='Puntos dentro de las curvas') ax.plot(puntos[2], puntos[3], 'o', label='Puntos fuera de las curvas') ax.legend() plt.show()

Run to view results

Entonces como resumen, nosotros generamos puntos aleatorios en un cuadrado y determinamos si cada punto está debajo de la línea o del semicírculo. Luego, se calcula el área estimada en función de la proporción de puntos que se encuenctran debajo de las curvas en comparación con el área total del cuadrado. y de esta manera visualización final que obtenemos muestra las funciones y los puntos generados, diferenciando entre puntos dentro y fuera de las curvas. Obteniendo la respuesta correcta y resaltando el area esperado

import numpy as np import matplotlib.pyplot as plt import pandas as pd # Define la ecuación de la línea def line_eq(x): return 0.5 * x # Define la ecuación del semicírculo con límites actualizados def semicircle_eq(x): return np.where((x >= 1.6) & (x <= 4), 4 - np.sqrt(4**2 - (x - 4)**2), 0) # Función para verificar si un punto (x, y) está debajo de la línea o el semicírculo def below_curves(x, y): if x < 1.6: return y < line_eq(x) else: return y < semicircle_eq(x) # Función para generar muestras aleatorias def realizar_muestra(a, b, n): return np.random.uniform(a, b, n) # Método de muestreo def sampling(a, b, c, n): x_m = realizar_muestra(a, b, n) y_m = realizar_muestra(0, c, n) # Verifica si cada punto está debajo de la curva below_curve_recta_mask = np.all(np.vstack([y_m < line_eq(x_m), x_m < 1.6]), axis=0) below_curve_semicirculo_mask = np.all(np.vstack([y_m < semicircle_eq(x_m), (x_m >= 1.6) & (x_m <= 4)]), axis=0) # Separa los puntos debajo de las curvas y los puntos fuera de las curvas x_dentro_recta = x_m[below_curve_recta_mask] y_dentro_recta = y_m[below_curve_recta_mask] x_dentro_semicirculo = x_m[below_curve_semicirculo_mask] y_dentro_semicirculo = y_m[below_curve_semicirculo_mask] x_fuera = x_m[~(below_curve_recta_mask | below_curve_semicirculo_mask)] y_fuera = y_m[~(below_curve_recta_mask | below_curve_semicirculo_mask)] return x_dentro_recta, y_dentro_recta, x_dentro_semicirculo, y_dentro_semicirculo, x_fuera, y_fuera # Parámetros (a, b, c) = (0, 4, 4) # Área del cuadrado area_cuadrado = (b - a) * c # Realiza el método de muestreo para diferentes valores de n t_muestras = [10, 100, 1000, 5000, 10000] # Inicializa listas para almacenar resultados resultados = [] for t in t_muestras: puntos = sampling(a, b, c, t) area_recta = len(puntos[0]) / t * area_cuadrado area_semicirculo = len(puntos[2]) / t * area_cuadrado resultados.append({ 'Tamaño de Muestra (n)': t, 'Área bajo la Recta': area_recta, 'Área bajo el Semicírculo': area_semicirculo, 'Puntos Fuera de las Curvas': len(puntos[4]) }) # Crea un DataFrame de pandas para mostrar los resultados en forma de tabla df_resultados = pd.DataFrame(resultados) # Muestra los resultados en forma de tabla print(df_resultados) # Grafica las áreas estimadas en función del tamaño de muestra fig, ax = plt.subplots(figsize=(8, 6)) ax.plot(df_resultados['Tamaño de Muestra (n)'], df_resultados['Área bajo la Recta'], label='Área bajo la Recta') ax.plot(df_resultados['Tamaño de Muestra (n)'], df_resultados['Área bajo el Semicírculo'], label='Área bajo el Semicírculo') ax.set_xlabel('Tamaño de Muestra (n)') ax.set_ylabel('Área Estimada') ax.legend() plt.show()

Run to view results

Ahora como metodo de representacion utilizamos la tabla, la misma que nos muestra como cambia el area de la curva segun la muestra que tenemos y imprimimos los puntos que no se encuentran dentro de ninguno de los dos

import numpy as np import matplotlib.pyplot as plt import seaborn as sns import pandas as pd # ... (Código de funciones y métodos previos) # Realizar el método de Hit and Miss para diferentes valores de n t_muestras = [10, 100, 1000, 5000, 10000] # Inicializar listas para almacenar resultados resultados_hit_and_miss = [] resultados_muestreo = [] for t in t_muestras: # Obtener los puntos generados y calcular el área para Hit and Miss puntos_hit_and_miss = hit_and_miss(a, b, c, t) area_hit_and_miss = len(puntos_hit_and_miss[0]) / t * area_cuadrado resultados_hit_and_miss.append({ 'Tamaño de Muestra (n)': t, 'Área bajo la Curva (Hit and Miss)': area_hit_and_miss, 'Puntos Fuera de las Curvas (Hit and Miss)': len(puntos_hit_and_miss[2]) }) # Obtener los puntos generados y calcular el área para el método de muestreo puntos_muestreo = sampling(a, b, c, t) area_muestreo = len(puntos_muestreo[0]) / t * area_cuadrado resultados_muestreo.append({ 'Tamaño de Muestra (n)': t, 'Área bajo la Curva (Muestreo)': area_muestreo, 'Puntos Fuera de las Curvas (Muestreo)': len(puntos_muestreo[4]) }) # Crear DataFrames de pandas para los resultados df_hit_and_miss = pd.DataFrame(resultados_hit_and_miss) df_muestreo = pd.DataFrame(resultados_muestreo) # Crear gráficos para visualizar los resultados sns.set(style="whitegrid") # Gráfico para Área bajo la Curva plt.figure(figsize=(12, 6)) plt.subplot(1, 2, 1) sns.lineplot(x='Tamaño de Muestra (n)', y='Área bajo la Curva (Hit and Miss)', data=df_hit_and_miss, label='Hit and Miss') sns.lineplot(x='Tamaño de Muestra (n)', y='Área bajo la Curva (Muestreo)', data=df_muestreo, label='Muestreo') plt.title('Área bajo la Curva por Tamaño de Muestra') plt.xlabel('Tamaño de Muestra (n)') plt.ylabel('Área bajo la Curva') plt.legend() # Gráfico para Puntos Fuera de las Curvas plt.subplot(1, 2, 2) sns.lineplot(x='Tamaño de Muestra (n)', y='Puntos Fuera de las Curvas (Hit and Miss)', data=df_hit_and_miss, label='Hit and Miss') sns.lineplot(x='Tamaño de Muestra (n)', y='Puntos Fuera de las Curvas (Muestreo)', data=df_muestreo, label='Muestreo') plt.title('Puntos Fuera de las Curvas por Tamaño de Muestra') plt.xlabel('Tamaño de Muestra (n)') plt.ylabel('Puntos Fuera de las Curvas') plt.legend() plt.tight_layout() plt.show()

Run to view results

Este código crea dos gráficos: uno para representar la variación del área bajo la curva con el tamaño de la muestra y otro para la cantidad de puntos fuera de las curvas. Como podemos ver en la grafica los resultados son casi iguales con pequeñas variciones

Conclusiones

Gracias a las simulaciones, podemos observar que el metodo de sampling, es mas preciso

El metodo de hit and miss presenta desafíos en términos de eficiencia computacional. Esto debido a que mientras mas se aumenta el número de puntos, el tiempo de ejecución tiende a aumentar significativamente. Esto puede limitar su utilidad en situaciones donde se requieren resultados precisos con una gran cantidad de puntos.

Recomendaciones

Agregar documentación y comentarios en el código para explicar la funcionalidad de las funciones y el propósito de cada bloque de código. Esto facilitará la comprensión del código, especialmente si alguien más lo revisa en el futuro.

Considerar la inclusión de manejo de errores y excepciones para garantizar que el código sea robusto y maneje situaciones inesperadas de manera adecuada.

En el caso de que ell código tarda mucho en ejecutarse con tamaños de muestra muy grandes, puedes explorar opciones de optimización de rendimiento, como el uso de técnicas vectorizadas en lugar de bucles.

Tener conocimiento, ambos metodos son bastantes complicados de elaborar, los mismos que son imposible en caso de no tener un conocimiento anterior o conocimientos basicos de estadistica

Bibliografia

Final_Project_MS202320_ERGGJCMVIO. (2023, 10 noviembre). Deepnote. https://deepnote.com/@udla-1dc7/FinalProjectMS202320ERGGJCMVIO-6c62f7af-27fd-4cf4-aa53-b3925c29f283

Garriga, A. (2020, 16 noviembre). Método de Montecarlo en proyectos. Recusos en project management. https://www.recursosenprojectmanagement.com/metodo-de-montecarlo/

¿Qué es la simulación Montecarlo? | IBM. (s. f.). https://www.ibm.com/es-es/topics/monte-carlo-simulation

Sánchez, S. (2023, 31 octubre). Qué es sampling: definición, ventajas de aplicarlo y ejemplos. https://aulacm.com/que-es/sampling-definicion-ejemplos/#:~:text=Cuando%20hablamos%20de%20sampling%20nos,ofrecemos%20tras%20probar%20c%C3%B3mo%20funciona.

.css-15w88e5{color:var(--chakra-colors-fg-neutral-primary);font-weight:inherit;letter-spacing:-0.09px;}Metodo de Monte Carlo

Introducción

Objetivos

Marco Teorico

Ventajas y desventajas del método Monte Carlo

Problema a resolver

Métodos a utilizar

Metodo de muestreo(sampling)

Metodo de hit and miss

Solucion

Metodo de Hit and Miss

Metodo de Sampling

Conclusiones

Recomendaciones

Bibliografia

Metodo de Monte Carlo